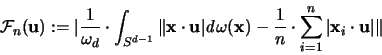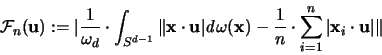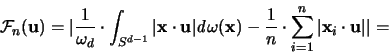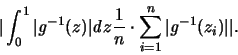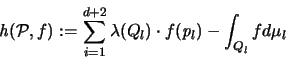Nächste Seite: Literatur
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Projektionskörper, Zonotope
Inhalt
In diesem Paragraphen wollen wir an das Problem des fünften
Paragraphen anknüpfen.
Die Ungleichung (III.5.8) von Betke-McMullen benützt auf der
linken Seite den Ausdruck:
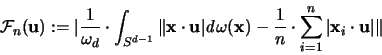 |
(3.36) |
Dieser Ausdruck bezeichnet den Fehler der Approximation des
Cauchy'schen Oberflächenintegrales durch dessen
korrespondierende Summe [55].
Die in diesem Ausdruck auftretende Summe ist gleich der
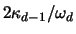 -fachen Stützfunktion des Zonotopes Z mit Generator
-fachen Stützfunktion des Zonotopes Z mit Generator
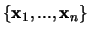 , das Integral ist nach (II.5) gleich
, das Integral ist nach (II.5) gleich 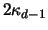 .
.
Daher ist
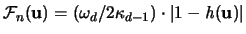 gleich einer Konstanten mal der Differenz von Kugelradius und Abstand des
Zonotopes in Richtung
gleich einer Konstanten mal der Differenz von Kugelradius und Abstand des
Zonotopes in Richtung 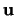 . Aus (III.5) folgt [
. Aus (III.5) folgt [
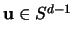 ]:
]:
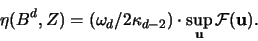 |
(3.37) |
Die Funktion
![$f: S^{d-1} \to [-1,+1]: {\mathbf x} \to {\mathbf x} \cdot {\mathbf u}$](img1014.gif) kann als
Orthogonalprojektion von
kann als
Orthogonalprojektion von  auf die Linie [-1,+1] betrachtet werden.
auf die Linie [-1,+1] betrachtet werden.
Diese Projektion soll so ''gestört'' werden, daß das Maß einer
beliebigen sphärischen Kappe
mit Mittelpunkt 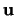 invariant bleibt.
invariant bleibt.
Die Oberfläche 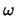 von
von
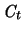 ist [55]
gegeben durch das Integral:
ist [55]
gegeben durch das Integral:
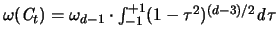
,
für d = 3 ist dies
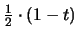
.
Es ist nun
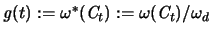 eine
streng fallende Funktion, die [-1,+1] auf [0,1] abbildet und die für
eine
streng fallende Funktion, die [-1,+1] auf [0,1] abbildet und die für 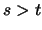 stets die Gleichung
stets die Gleichung
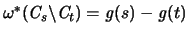 erfüllt.
Die Funktion
erfüllt.
Die Funktion
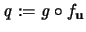 bildet
bildet  auf [0,1] ab und ist in folgendem Sinne maßtreu:
auf [0,1] ab und ist in folgendem Sinne maßtreu:
für jedes Intervall
![${\mathit I} \subset [0,1]$](img1023.gif) und für das
Lebesguemaß
und für das
Lebesguemaß  gilt:
gilt:
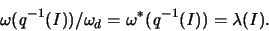 |
(3.38) |
Diese Maßtreue ist ersichtlich aus:
Wegen
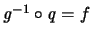 impliziert die Maßtreue:
impliziert die Maßtreue:
Um dies einsehen zu können, benötigt man den
Integraltransformationssatz der Maßtheorie:
Es seien
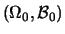 und
und
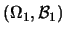 zwei Meßräume,
zwei Meßräume,
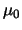 sei ein Maß auf
sei ein Maß auf
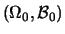 ,
,
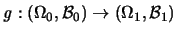 und
und
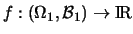 seien zwei Funktionen. Dann ist:
seien zwei Funktionen. Dann ist:
Das durch
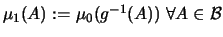 definierte Maß
nennt man Bildmaß von
definierte Maß
nennt man Bildmaß von 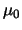 unter der Abbildung g.
unter der Abbildung g.
Setzen wir
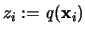 , so ist:
, so ist:
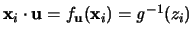 .
Aufgrund der Invarianzgleichung schreibt sich
.
Aufgrund der Invarianzgleichung schreibt sich
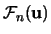 an als:
an als:
Das bedeutet, daß wir
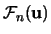 als den Fehler einer
eindimensionalen numerischen Integration betrachten können, auf den wir
die Ungleichung von Koksma (II.1) ( s.[48]) anwenden.
als den Fehler einer
eindimensionalen numerischen Integration betrachten können, auf den wir
die Ungleichung von Koksma (II.1) ( s.[48]) anwenden.
Die totale Variation
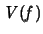 einer stetigen und monotonen
Funktion auf einem Intervall ist gleich der Differenz der Beträge
der Intervallenden. In unserem Fall ist
einer stetigen und monotonen
Funktion auf einem Intervall ist gleich der Differenz der Beträge
der Intervallenden. In unserem Fall ist
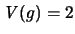 und wir
erhalten aus der Ungleichung von Koksma [55]:
und wir
erhalten aus der Ungleichung von Koksma [55]:
Also ist der Fehler kleiner gleich der zweifachen
Sterndiskrepanz in Bezug auf Intervalle der Form [0,a] mit
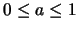 .
Da wir mit
.
Da wir mit
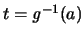 auch
auch
![${\mathit q}^{-1}([0,a]) =
{\mathbf{\mathit C}}_t $](img1046.gif) und
und
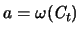 haben, gilt mit
haben, gilt mit
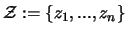 und
und ![$a \in [0,1]$](img1049.gif) :
:
Also können wir
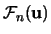 abschätzen durch die sphärische
Kappendiskrepanz von (II.2). Wir brauchen nur das dortige Ergebnis zu
übernehmen und erhalten so den Satz:
abschätzen durch die sphärische
Kappendiskrepanz von (II.2). Wir brauchen nur das dortige Ergebnis zu
übernehmen und erhalten so den Satz:
Für jede natürliche Zahl 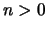 gibt es eine Menge von Punkten
gibt es eine Menge von Punkten
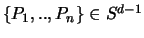 , sodaß gilt:
, sodaß gilt:
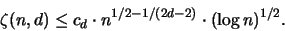 |
(3.39) |
Die Beck'sche Methode kann man aber auch direkt auf unsere
Aufgabenstellung anwenden [11]:
Für jede beliebige ganze Zahl n sei
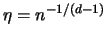 Wir zerlegen analog zu (II.2) die
Wir zerlegen analog zu (II.2) die  in n kompakte, zusammenhängende
und paarweise disjunkte Mengen
in n kompakte, zusammenhängende
und paarweise disjunkte Mengen
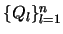 . Das Lebesguemaß von
jeder dieser Mengen sei
. Das Lebesguemaß von
jeder dieser Mengen sei 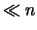 und ihr Durchmesser sei
und ihr Durchmesser sei
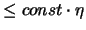 .
.
In jedem 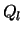 wählen wir zufällig und unabhängig voneinander
d+2 Punkte aus. Dann hat für jede stetige Funktion f auf
wählen wir zufällig und unabhängig voneinander
d+2 Punkte aus. Dann hat für jede stetige Funktion f auf  bei geeignetem Maß
bei geeignetem Maß 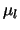 auf
auf 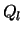 der Ausdruck
der Ausdruck
einen Betrag
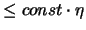 .
.
Durch die Anwendung der Bernstein'schen Ungleichung und durch
Einsetzen der obigen Werte erhält man den Satz [11]:
Für 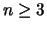 gibt es stets ein Zonotop und eine Konstante
gibt es stets ein Zonotop und eine Konstante 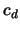 mit:
mit:
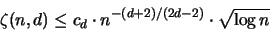 |
(3.40) |
Die Güte der gefundenen Abschätzung bestätigt uns :
s gibt für 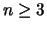 stets eine Konstante
stets eine Konstante 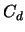 und ein Zonotop mit:
und ein Zonotop mit:
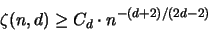 |
(3.41) |
Zum Beweis ( s.[12],[13]) verwenden wir ein positives und
symmetrisches Maß 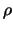 auf
auf  . Das heißt, es ist für alle
. Das heißt, es ist für alle  auf der
auf der
 größer Null und weiters ist
größer Null und weiters ist
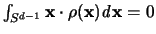 .
.
Es ist dann
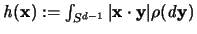 die Stützfunktiom eines konvexen Körpers. Ist
die Stützfunktiom eines konvexen Körpers. Ist 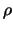 ein diskretes Maß,
so ist
ein diskretes Maß,
so ist 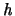 die Stützfunktion eines Zonotopes.
die Stützfunktion eines Zonotopes.
Die Funktion 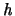 läßt sich in der Theorie der sphärischen
Fourieranalyse [67] darstellen als
läßt sich in der Theorie der sphärischen
Fourieranalyse [67] darstellen als 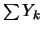 . Die Funktion
. Die Funktion 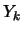 ist dabei
eine sphärische harmonische Funktion von Ordnung k.
Die
ist dabei
eine sphärische harmonische Funktion von Ordnung k.
Die 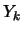 's erfüllen folgende Orthogonalitätsrelation [67]:
's erfüllen folgende Orthogonalitätsrelation [67]:
Der Theorie der sphärischen harmonischen Analyse entnimmt man
[12,13,67], daß man das Maß 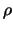 formal anschreiben kann als:
formal anschreiben kann als:
Die 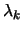 's sind dabei geeignete Gewichte der Ordnung
's sind dabei geeignete Gewichte der Ordnung
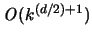 .
.
Für 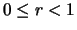 setzen wir
setzen wir
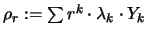 [12].
Aufgrund der Orthogonalität der
[12].
Aufgrund der Orthogonalität der 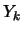 's gilt der Satz von Pythagoras und damit:
's gilt der Satz von Pythagoras und damit:
Es sei 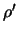 ein zweites Maß auf
ein zweites Maß auf  , das dieselben
Eigenschaften wir
, das dieselben
Eigenschaften wir 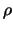 besitzt. Analog zu oben bilden wir die zu
besitzt. Analog zu oben bilden wir die zu 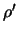 zugehörigen Funktionen
zugehörigen Funktionen 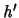 ,
,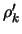 und
und 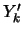 und können dann
das Quadrat des
und können dann
das Quadrat des 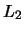 -Abstandes dieser beiden Maße abschätzen durch:
-Abstandes dieser beiden Maße abschätzen durch:
Also ist:
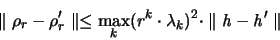 |
(3.42) |
Wegen
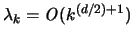 läßt sich das Maximum abschätzen durch:
läßt sich das Maximum abschätzen durch:
Die Funktion
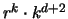 hat ihr Maximum an der Stelle
hat ihr Maximum an der Stelle
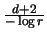 wie man durch Differentiation und aus
Monotonieüberlegungen ersieht. (Man beachte, daß für
wie man durch Differentiation und aus
Monotonieüberlegungen ersieht. (Man beachte, daß für 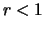 der Logarithmus negativ, und damit der Ausdruck
der Logarithmus negativ, und damit der Ausdruck 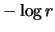 positiv ist.)
Es ist somit:
positiv ist.)
Es ist somit:
Da die Funktion 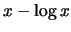 auf [0,1] monoton fällt, ist
auf [0,1] monoton fällt, ist
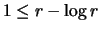 und damit:
und damit:
Also haben wir:
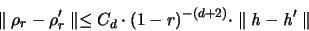 |
(3.43) |
Es sei nun 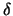 das durch
das durch
 induzierte Maß.
Es hat für
induzierte Maß.
Es hat für
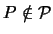 den Wert Null und für
den Wert Null und für
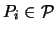 ist
ist
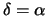 . Diese Werte
. Diese Werte 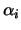 sind alle positiv und so gewählt,
daß gilt:
sind alle positiv und so gewählt,
daß gilt:
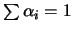 .
Für das induzierte Maß
.
Für das induzierte Maß 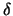 und das Oberflächenmaß
und das Oberflächenmaß 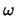 kann man
zeigen [12,13], daß für
kann man
zeigen [12,13], daß für
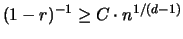 mit einer Konstanten C gilt:
mit einer Konstanten C gilt:
Damit können wir den Beweis von (3.41) vervollständigen. Denn es gilt [12,13]:




Nächste Seite: Literatur
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Projektionskörper, Zonotope
Inhalt
2004-03-25