



Nächste Seite: Projektionskörper, Zonotope
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Zufallspolyeder
Inhalt
In III.2 bewiesen wir, daß es zu jedem konvexen Körper K ein
Polyeder mit beliebig kleinem Hausdorffabstand gibt. Nichts
hingegen wurde ausgesagt über die Struktur des Polyeders.
Klarerweise wird die Approximation des konvexen Körpers K
durch das bestapproximierende Polyeder 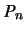 mit n Flächen
(oder n Ecken) für wachsendes n immer besser, da dann der
Hausdorffabstand für wachsendes n nach Null strebt.
mit n Flächen
(oder n Ecken) für wachsendes n immer besser, da dann der
Hausdorffabstand für wachsendes n nach Null strebt.
Die Approximation erfolgt dabei mit Größenordnung 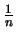 , das
heißt, daß sich
, das
heißt, daß sich
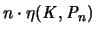 einem Grenzwert
einem Grenzwert
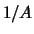 nähert.
nähert.
Dieses A wollen wir die Approximierbarkeit von K nennen.
Dieser Begriff wurde von Fejes-Tóth in [30] eingeführt, und von
R.Schneider in [73] umfassend behandelt. Er erhält dabei den
folgenden Satz:
Es sei 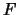 eine geschlossene konvexe Hyperfläche der
Differentiationsklasse
eine geschlossene konvexe Hyperfläche der
Differentiationsklasse
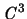 (dh.
(dh. 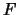 ist der Rand eines kompakten konvexen
Körpers und ist mindestens dreimal stetig differenzierbar).
ist der Rand eines kompakten konvexen
Körpers und ist mindestens dreimal stetig differenzierbar).
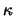 bezeichne die (positive) Gauß'sche Krümmung der Fläche
bezeichne die (positive) Gauß'sche Krümmung der Fläche 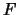 ,
,
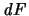 sei ihr Oberflächenelement in der zweiten Grundform.
sei ihr Oberflächenelement in der zweiten Grundform.
Für 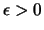 sei
sei 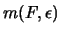 die kleinste natürliche Zahl mit der
Eigenschaft, daß es ein der Fläche F eingeschriebenes konvexes Polytop P
mit m Ecken gibt, für das
die kleinste natürliche Zahl mit der
Eigenschaft, daß es ein der Fläche F eingeschriebenes konvexes Polytop P
mit m Ecken gibt, für das
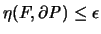 ist.
ist.
Ist ferner 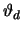 die Dichte der dünnsten Überdeckung des
d-dimensionalen Raumes durch Einheitskugeln, so gilt :
die Dichte der dünnsten Überdeckung des
d-dimensionalen Raumes durch Einheitskugeln, so gilt :
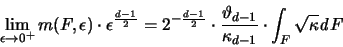 |
(3.20) |
Der exakte Wert von 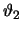 ist bekannt:
ist bekannt:
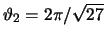 [72]. Daher können wir für d = 3 schreiben:
[72]. Daher können wir für d = 3 schreiben:
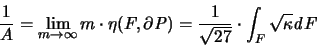 |
(3.21) |
Der Satz besagt, daß man die Approximierbarkeit eines
konvexen Körpers allein aus seiner Gauß'schen Krümmung berechnen
kann. Weiters folgt daraus, daß unter allen konvexen Körpern
die Kugel am schlechtesten approximierbar ist.
Der Beweis des Satzes bedarf vieler technischer Hilfsmittel.
Seine Grundidee ist die, die Fläche durch sogenannte
II-geodätische Kreise, das sind Kreise in der durch die zweite
Fundamentalform induzierten Metrik, zu überdecken.
Bekanntlich läßt sich die Gauß'sche Krümmung berechnen durch:
Die auftretenden Koeffizienten sind dabei die Koeffizienten der
ersten Grundform [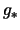 ] sowie die der zweiten Grundform [
] sowie die der zweiten Grundform [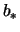 ].
].
Ist
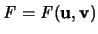 eine Parameterdarstellung
der Fläche F, so lassen sich diese Koeffizienten errechnen aus :
eine Parameterdarstellung
der Fläche F, so lassen sich diese Koeffizienten errechnen aus :
Ist 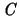 eine Kurve in F, so ist ihre II-Länge gegeben durch das
Integral:
eine Kurve in F, so ist ihre II-Länge gegeben durch das
Integral:
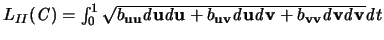 geeignet parametrisiet:
geeignet parametrisiet:
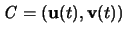 .,
.,
Sind zwei Punkte 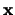 und
und 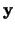 auf F gegeben, so definieren mit
uns die II-Metrik
auf F gegeben, so definieren mit
uns die II-Metrik 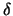 als das Infimum über die II-Länge aller
Kurven
als das Infimum über die II-Länge aller
Kurven 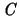 , die
, die 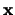 und
und 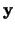 verbinden. Damit können wir eine
II-Kugel um
verbinden. Damit können wir eine
II-Kugel um 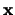 mit Radius
mit Radius 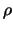 definieren durch
definieren durch
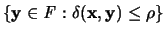 .
.
Bezeichnet man mit
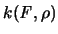 die kleinste natürliche Zahl, die
eine Überdeckung von F durch derartige Kreise zuläßt, so gilt
für
die kleinste natürliche Zahl, die
eine Überdeckung von F durch derartige Kreise zuläßt, so gilt
für
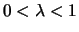 und für genügend kleines
und für genügend kleines 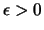 :
([73], Hilfssatz 2).
:
([73], Hilfssatz 2).
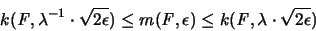 |
(3.22) |
Der Beweis der linken Ungleichung geht von der Fläche F und
einem ''passenden'' Polytop aus. Man betrachtet dann die zu einer
Tangentialebene parallele Ebene im Abstand 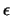 und zeigt, daß der
Punkt, an den die Ebene gelegt wurde, in einer II-Kugel mit Radius
und zeigt, daß der
Punkt, an den die Ebene gelegt wurde, in einer II-Kugel mit Radius
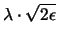 um einen Eckpunkt des Polytopes liegen muß.
um einen Eckpunkt des Polytopes liegen muß.
In umgekehrter Richtung gibt man sich eine Überdeckung durch
m II-Kugeln vor, bildet die konvexe Hülle der Mittelpunkte und
zeigt auf indirekte Weise, daß dieses Polytop P einen genügend
kleinen Abstand
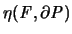 besitzt.
besitzt.
Der zentrale Beweisschritt des Satzes liegt in dem Lemma:
Ist 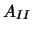 (M) das (d-1)-dimensionale Volumen einer offenen
Teilmenge
(M) das (d-1)-dimensionale Volumen einer offenen
Teilmenge
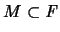 bezüglich der durch die zweite Grundform induzierten
Metrik, und ist
bezüglich der durch die zweite Grundform induzierten
Metrik, und ist
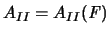 , so gilt [73,Hilfssatz 4]:
, so gilt [73,Hilfssatz 4]:
Mit diesen Elementen kann der Beweis vervollständigt werden:
Zunächt bemerken wir, daß
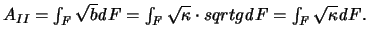 Sodann gilt für
Sodann gilt für 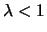 die Gleichungskette (s. Lemma und Hilfssatz 2):
die Gleichungskette (s. Lemma und Hilfssatz 2):
Aus
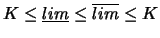 und aus
und aus
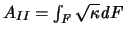 folgt für
folgt für
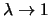 die Behauptung des Satzes
die Behauptung des Satzes 
In [37] wird ein analoger Satz für die symmetrische
Differenzmetrik bewiesen. Bis auf geänderte Konstante wird auch
dort die Approximationsgeschwindigkeit von 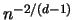 erhalten.
erhalten.




Nächste Seite: Projektionskörper, Zonotope
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Zufallspolyeder
Inhalt
2004-03-25
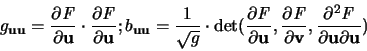
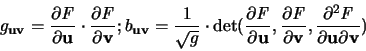
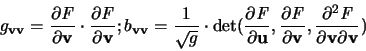
![]() (M) das (d-1)-dimensionale Volumen einer offenen
Teilmenge
(M) das (d-1)-dimensionale Volumen einer offenen
Teilmenge
![]() bezüglich der durch die zweite Grundform induzierten
Metrik, und ist
bezüglich der durch die zweite Grundform induzierten
Metrik, und ist
![]() , so gilt [73,Hilfssatz 4]:
, so gilt [73,Hilfssatz 4]: