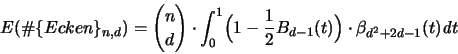Nächste Seite: Approximierbarkeit konvexer Körper
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Approximation durch Polyeder
Inhalt
Eine erste Möglichkeit, Polyeder mit Kugel zu kombinieren,
haben wir bereits im ersten Kapitel kennengelernt und im
vorigen Paragraphen genauer betrachtet.
Bevor wir der Frage nachgehen, wie gut sich die Kugel durch
Polyeder approximeren läßt, wollen wir den Erwartungswert
bestimmter Maßzahlen eines Zufallspolyeders ermitteln. Darunter
verstehen wir die konvexe Hülle von n zufällig ausgewählten
Punkten auf der  .
.
Will man n Punkte gemäß einer Wahrscheinlichkeitsverteilung
auf der Sphäre auswählen, so muß man sich zuerst
überlegen, auf welche Weise dies möglich ist. Üblicherweise wird dazu
die Sphäre mit Polarkoordinaten ausgestattet.
Wir können annehmen, daß die gewünschte Verteilung eine
gewöhnliche mehrdimensionale Dichte besitzt. Für die
Gleichverteilung muß wegen
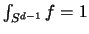 die Dichte
die Dichte
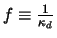 sein.
sein.
Es seien nun gemäß der Gleichverteilung n Punkte auf der
 ausgewählt. In [15] wird der Erwartungswert der drei Maßzahlen
Oberfläche, mittlere Breite und Anzahl der Seiten berechnet.
Da die dabei erhaltenen Formeln zwar exakt, aber kompiliziert sind,
werden auch einfachere asymptotische Abschätzungen aus ihnen
hergeleitet.
ausgewählt. In [15] wird der Erwartungswert der drei Maßzahlen
Oberfläche, mittlere Breite und Anzahl der Seiten berechnet.
Da die dabei erhaltenen Formeln zwar exakt, aber kompiliziert sind,
werden auch einfachere asymptotische Abschätzungen aus ihnen
hergeleitet.
Die zugrundeliegende Denkweise soll im folgenden anhand der
Oberfläche erläutert werden.
Es ist zunächst zu bemerken, daß bei statistischen
Überlegungen nur Polytope, deren Facetten Simplizes sind, eine
Rolle spielen, da andere Polytoptypen nur mit Wahrscheinlichkeit
Null auftreten können.
Unter einer Facette eines d-dimensionalen Polytopes P
versteht man stets die (d-1)-dimensionalen Flächen von P.
Daher können wir die Oberfläche der konvexen Hülle der Punkte
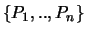 als Summe d-eckiger Facetten betrachten.
als Summe d-eckiger Facetten betrachten.
Wählen wir aus
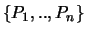 auf beliebige Weise d Punkte aus,
die wir o.B.d.A. stets mit
auf beliebige Weise d Punkte aus,
die wir o.B.d.A. stets mit 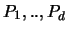 bezeichnen wollen, so ist
die konvexe Hülle der d Punkte
bezeichnen wollen, so ist
die konvexe Hülle der d Punkte 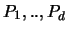 genau dann eine
Facette eines konvexen, d-dimensionalen und n-eckigen Polytops,
wenn die übrigen (n-d) Punkte
genau dann eine
Facette eines konvexen, d-dimensionalen und n-eckigen Polytops,
wenn die übrigen (n-d) Punkte
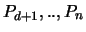 auf ein und derselben
Seite der Hyperebene
auf ein und derselben
Seite der Hyperebene 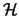 zu liegen kommen, die durch
zu liegen kommen, die durch 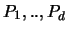 aufgespannt wird.
aufgespannt wird.
Diese Hyperebene
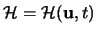 zerlegt die Vollkugel
zerlegt die Vollkugel 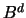 in zwei Kugelkappen, eine mit Höhe 1-t und eine mit Höhe 1+t. Dabei
bezeichnet t den Abstand der Hyperebene zum Ursprung.
in zwei Kugelkappen, eine mit Höhe 1-t und eine mit Höhe 1+t. Dabei
bezeichnet t den Abstand der Hyperebene zum Ursprung.
Wird mit
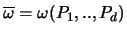 die Oberfläche der
kleineren Kugelkappe bezeichnet, so ist die Wahrscheinlichkeit, daß ein Punkt
auf diesem Teil der Kugel liegt, gleich
die Oberfläche der
kleineren Kugelkappe bezeichnet, so ist die Wahrscheinlichkeit, daß ein Punkt
auf diesem Teil der Kugel liegt, gleich
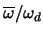 , das ist
Kugelkappenoberfläche/Gesamtkugeloberfläche. Die Wahrscheinlichkeit,
daß er auf der anderen Kugelkappe liegt, ist gleich der
Gegenwahrscheinlichkeit
, das ist
Kugelkappenoberfläche/Gesamtkugeloberfläche. Die Wahrscheinlichkeit,
daß er auf der anderen Kugelkappe liegt, ist gleich der
Gegenwahrscheinlichkeit
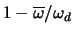 .
.
Die  's sind gleichmäßig und unabhängig voneinander über
's sind gleichmäßig und unabhängig voneinander über
 verteilt, und daher tritt das Ereignis, daß alle n-d Punkte
verteilt, und daher tritt das Ereignis, daß alle n-d Punkte
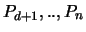 vollständig in einem der beiden Kugelteile liegen,
mit Wahrscheinlichkeit
vollständig in einem der beiden Kugelteile liegen,
mit Wahrscheinlichkeit 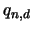 ein:
ein:
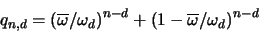 |
(3.14) |
Die Wahrscheinlichkeit 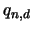 hängt klarerweise nur von den
Parametern der Trägerhyperebene ab, da eine Veränderung der
Punkte innerhalb dieser Hyperebene keinen Einfluß auf den
Abstand der Hyperebene vom Ursprung der
hängt klarerweise nur von den
Parametern der Trägerhyperebene ab, da eine Veränderung der
Punkte innerhalb dieser Hyperebene keinen Einfluß auf den
Abstand der Hyperebene vom Ursprung der  besitzt. Daher
können wir
besitzt. Daher
können wir 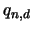 als Funktional der Hyperebenenparameter
als Funktional der Hyperebenenparameter 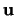 und t betrachten:
und t betrachten:
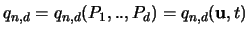 .
.
Weiters sei folgende Konvention eingeführt: Um die folgenden
Formeln übersichtlich gestalten zu können, schreiben wir unter
das Integralzeichen immer nur die Variable, für die das Zeichen
gilt. Integriert wir immer über  . Bei reellen
Integrationsparametern wird wie üblich das Integrationsintervall angegeben.
. Bei reellen
Integrationsparametern wird wie üblich das Integrationsintervall angegeben.
Die Punkte 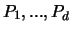 spannen im
spannen im
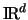 ein (d-1)-dimensionales
Simplex auf, dessen Inhalt
ein (d-1)-dimensionales
Simplex auf, dessen Inhalt
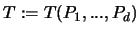 sei. Dann ist:
sei. Dann ist:
der Erwartungswert des Volumens der Facette
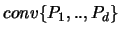 .
Da es stets
.
Da es stets
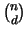 Möglichkeiten gibt, aus n Punkten d auszuwählen,
gilt für den Erwartungswert der Gesamtoberfläche
Möglichkeiten gibt, aus n Punkten d auszuwählen,
gilt für den Erwartungswert der Gesamtoberfläche 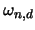 :
:
Gemäß [64] kann man die unabhängige und gleichverteilte
Auswahl von d Punkten auf der  stochastisch äquivalent durch
folgende sequentielle Konstruktion ersetzen :
stochastisch äquivalent durch
folgende sequentielle Konstruktion ersetzen :
(i) Wähle eine Trägerhyperebene
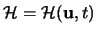 mit dem als
Sphärenelement gleichmäßig verteilten Normalvektor
mit dem als
Sphärenelement gleichmäßig verteilten Normalvektor 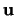 und mit
dem Abstand t vom Mittelpunkt der
und mit
dem Abstand t vom Mittelpunkt der  .
.
Dieser besitze als Zufallsvariable (
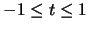 ) die Dichte:
) die Dichte:
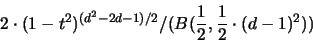 |
(3.15) |
Mit 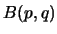 wird hier die Beta-Verteilung mit den Parametern p
und q bezeichnet. Im folgenden werden wir stets die Abkürzung
wird hier die Beta-Verteilung mit den Parametern p
und q bezeichnet. Im folgenden werden wir stets die Abkürzung
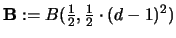 verwenden.
verwenden.
(ii) Der Schnitt dieser Hyperebene mit der Sphäre ist der
Rand einer (d-1)-dimensionalen Vollkugel mit Radius
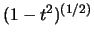 ,
deren sphärisches, (d-2)-dimensionales Oberflächenmaß im
weiteren mit
,
deren sphärisches, (d-2)-dimensionales Oberflächenmaß im
weiteren mit 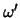 bezeichnet wird.
bezeichnet wird.
Da die Oberfläche einer d-dimensionalen Kugel mit Radius r
gegeben ist durch
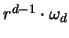 , ist
, ist
(iii) Wähle nun d Punkte 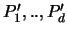 aus dem Schnitt von
aus dem Schnitt von  und
und
 . Die Auswahl der Punkte
. Die Auswahl der Punkte 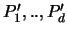 erfolge dabei gemäß einer
gemeinsamen Gleichverteilung mit der Gewichtung
erfolge dabei gemäß einer
gemeinsamen Gleichverteilung mit der Gewichtung
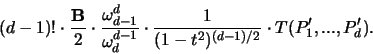 |
(3.16) |
Es ist bei diesen Dichten zu beachten, daß die auftretenden
Oberflächenmaße auf 1 zu normieren sind, um Wahrscheinlichkeitsmaße
zu erhalten. Daher wird 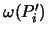 im folgenden stets
durch
im folgenden stets
durch
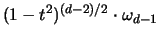 dividiert.
dividiert.
Die Auswahl von 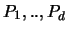 erfolgt also gemäß einer Dichte,
die gleich ist dem Produkt der beiden Dichten (2) und (3).
Daher ist:
erfolgt also gemäß einer Dichte,
die gleich ist dem Produkt der beiden Dichten (2) und (3).
Daher ist:
Damit kann der Erwartungswert
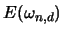 umgeformt werden zu:
umgeformt werden zu:
Da die Wahrscheinlichkeit 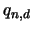 nur von der Trägerhyperebene
nur von der Trägerhyperebene  abhängt, können wir
abhängt, können wir 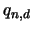 aus dem Integral über die P's herausziehen,
da sich diese nur innerhalb
aus dem Integral über die P's herausziehen,
da sich diese nur innerhalb 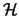 bewegen. Das ergibt:
bewegen. Das ergibt:
Als nächstes wollen wir den Wert des Integrals über 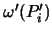 bestimmen, und nehmen uns dazu das zweite Moment folgender
Zufallsvariable zu Hilfe:
bestimmen, und nehmen uns dazu das zweite Moment folgender
Zufallsvariable zu Hilfe:
Das (d-1)-dimensionale Volumen der konvexen Hülle von d Punkten,
die auf der Oberfläche einer (d-1)-dimensionalen Kugel mit
Radius r liegen, habe die Dichtefunktion f. Es ist dann [64]:
Mit der entsprechenden Gewichtung erhält man daraus [15]:
Wenn wir dieses Resultat in die Formel für den Erwartungswert
einsetzen, ergibt dies:
Es wurde bereits bemerkt, daß
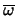 die Oberfläche einer d-
dimensionalen Kugelkappe mit Höhe 1-t ist. Man kann die
Oberfläche ausdrücken durch [15]:
die Oberfläche einer d-
dimensionalen Kugelkappe mit Höhe 1-t ist. Man kann die
Oberfläche ausdrücken durch [15]:
Damit erhält man:
Das innere Integral (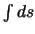 ) kann durch partielles Integrieren
und explizites Ausrechnen noch umgeformt werden [15]:
) kann durch partielles Integrieren
und explizites Ausrechnen noch umgeformt werden [15]:
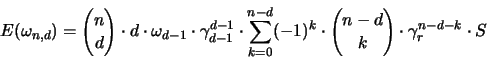 |
(3.17) |
Um diese Formel übersichtlicher gestalten zu können, wurden
folgende Abkürzungen verwendet :
Dabei ist
![$[c_0,c_1 ,..,c_l]^k_j$](img875.gif) der j-te Koeffizient von:
der j-te Koeffizient von:
Weiters setzt man 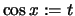 und:
und:
Das asymptotische Verhalten ist für die Oberfläche gleich:
hat also einen Fehlbetrag der Ordnung
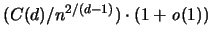 .
.
Weiters wird in [15] der Erwartungswert der Seitenanzahl der
konvexen Hülle behandelt. Die asymptotische Abschätzung lautet
bei dieser Fragestellung:
Eine ähnliche Fragestellung wird in [45] untersucht.
Autoren betrachten hier den Tangentialkörper, der aus n Punkten,
die auf der  liegen, gebildet wird und fragen nach
seiner zu erwartenden Eckenanzahl. Sie erhalten:
liegen, gebildet wird und fragen nach
seiner zu erwartenden Eckenanzahl. Sie erhalten:
wo
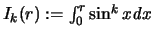 und
und
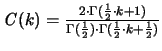 zu setzen ist.
zu setzen ist.
Ist 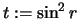 und bezeichnen wir mit
und bezeichnen wir mit 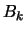 die Verteilungs- und
mit
die Verteilungs- und
mit 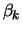 die Dichtefunktion der
die Dichtefunktion der 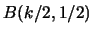 - Verteilung, so kann
man das Ergebnis auch anschreiben als:
- Verteilung, so kann
man das Ergebnis auch anschreiben als:
Für d = 3 gibt es ein exaktes Resultat:
Für größere Dimensionen ist auch hier eine Abschätzung
interessanter als die genaue Formel. In [45] findet man
mit Konstanten 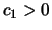 und
und 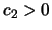 :
:
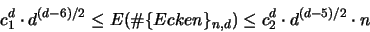 |
(3.18) |
In [14] befindet sich die genaue asymptotische Aussage:
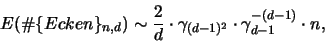 |
(3.19) |
Dabei ist
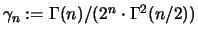 für
für
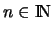 .
.




Nächste Seite: Approximierbarkeit konvexer Körper
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Approximation durch Polyeder
Inhalt
2004-03-25
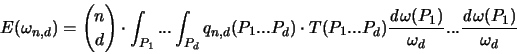
![]() , ist
, ist
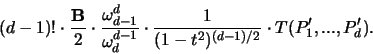
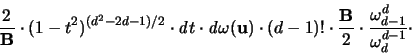
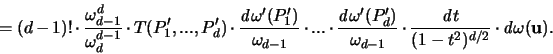
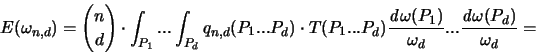
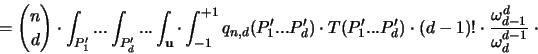
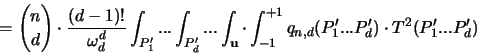
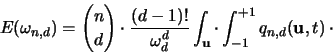
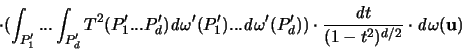
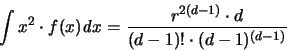
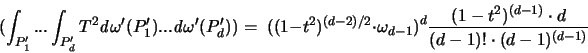
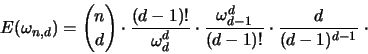
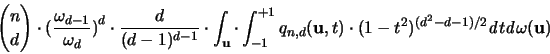
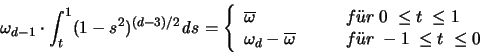
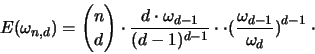
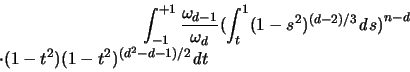
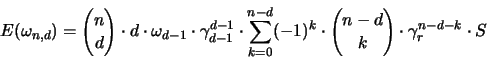
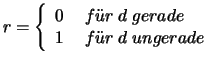
![\begin{displaymath}
\bigl( \sum_{i=0}^l c_i \cdot x^i \bigr) ^k =
\sum [c_0...c_r]_j^k \cdot x^j
\end{displaymath}](img876.gif)
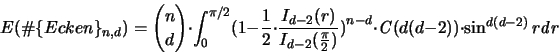
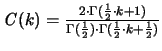 zu setzen ist.
zu setzen ist.