



Nächste Seite: Aus der Polyedergeometrie
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Lagerungen auf der 3-Sphäre
Inhalt
Im Jahre 1930 entdeckte der Biologe Tammes [83], daß sich
auf Pollenkörnern die Austrittsöffnungen der Pflanzenkeime so
anordnen, daß der Minimalabstand zwischen je zwei von ihnen
möglichst groß wird [''Tammes'sches Problem'' ] [ s.29,30,63,83].
Die zugrundeliegende Fragestellung lautet:
Wie kann man auf der Kugel n Punkte so verteilen, daß
der Minimalabstand zwischen je zwei von ihnen möglichst groß wird ?
Umgekehrt kann man sich die Frage stellen:
Wie kann man auf
der Kugel n Punkte so verteilen, daß der (sphärische) Abstand
von jedem beliebigen Punkt der Kugel zu einem der gegebenen
Punkte möglichst klein wird ?
Der sphärische Minimalabstand in der ersten Fragestellung
sei 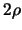 . Dann können wir um jeden der n Punkte einen (offenen)
Kreis mit Radius
. Dann können wir um jeden der n Punkte einen (offenen)
Kreis mit Radius 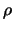 legen, sodaß niemals zwei dieser Kreise
einen inneren Punkt gemeinsam haben. Ein beliebiger Punkt der
Kugel kann dann zu höchstens einem Kreis gehören.
Beim zweiten Problem können wir um jeden der n Punkte einen
(abgeschlossenen) Kreis mit Radius
legen, sodaß niemals zwei dieser Kreise
einen inneren Punkt gemeinsam haben. Ein beliebiger Punkt der
Kugel kann dann zu höchstens einem Kreis gehören.
Beim zweiten Problem können wir um jeden der n Punkte einen
(abgeschlossenen) Kreis mit Radius 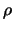 ziehen, sodaß jeder Punkt
der Kugeloberfläche mindestens einem der Kreise angehört.
Auf der Sphäre heißt eine Menge von (offenen) Kreisen
Unterdeckung der Sphäre, wenn jeder Punkt der Sphäre
höchstens einem Kreis angehört. Eine Menge von (abgeschlossenen)
Kreisen auf der Sphäre heißt Überdeckung der Sphäre,
wenn jeder Punkt der Sphäre zu mindestens einem Kreis gehört.
Um die Dichte einer Lagerung, das heißt die Dichte einer
Unter- oder einer Überdeckung, zu berechnen, berechnen wir die
Summe der Oberflächen der Kreise der Lagerung und dividieren
dann durch die Gesamtoberfläche der Kugel, das ist
ziehen, sodaß jeder Punkt
der Kugeloberfläche mindestens einem der Kreise angehört.
Auf der Sphäre heißt eine Menge von (offenen) Kreisen
Unterdeckung der Sphäre, wenn jeder Punkt der Sphäre
höchstens einem Kreis angehört. Eine Menge von (abgeschlossenen)
Kreisen auf der Sphäre heißt Überdeckung der Sphäre,
wenn jeder Punkt der Sphäre zu mindestens einem Kreis gehört.
Um die Dichte einer Lagerung, das heißt die Dichte einer
Unter- oder einer Überdeckung, zu berechnen, berechnen wir die
Summe der Oberflächen der Kreise der Lagerung und dividieren
dann durch die Gesamtoberfläche der Kugel, das ist 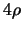 .
s.[29]
Da sich der Inhalt einer Kugelkappe mit Radius
.
s.[29]
Da sich der Inhalt einer Kugelkappe mit Radius 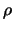 ausdrücken
läßt durch
ausdrücken
läßt durch
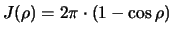 ,
gilt für die Dichte einer Lagerung von n kongruenten Kreisen:
,
gilt für die Dichte einer Lagerung von n kongruenten Kreisen:
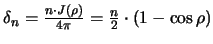 .
Da wir nur Lagerungen kongruenter Kreise betrachten, so
vereinbaren wir, daß eine '' Unterdeckung vom Radius r '' stets eine
Unterdeckung der Sphäre durch kongruente Kreise vom Radius r
sei und daß eine '' Überdeckung vom Radius R '' stets eine
Überdeckung der Sphäre durch kongruente Kreise vom Radius R sei.
Wir suchen nun also zu jeder natürlichen Zahl
.
Da wir nur Lagerungen kongruenter Kreise betrachten, so
vereinbaren wir, daß eine '' Unterdeckung vom Radius r '' stets eine
Unterdeckung der Sphäre durch kongruente Kreise vom Radius r
sei und daß eine '' Überdeckung vom Radius R '' stets eine
Überdeckung der Sphäre durch kongruente Kreise vom Radius R sei.
Wir suchen nun also zu jeder natürlichen Zahl ![$n [>2]$](img11.gif) die
Unterdeckung der Sphäre durch n kongruente Kreise mit größtmöglichem
Radius und größtmöglicher Dichte.
Weiters suchen wir zu jedem n die bestmögliche (optimale)
Überdeckung der Sphäre, das heißt die Überdeckung mit
kleinstmöglichem Radius und kleinstmöglicher Dichte.
Den Radius der optimalen Unterdeckung bezeichnen wir mit
die
Unterdeckung der Sphäre durch n kongruente Kreise mit größtmöglichem
Radius und größtmöglicher Dichte.
Weiters suchen wir zu jedem n die bestmögliche (optimale)
Überdeckung der Sphäre, das heißt die Überdeckung mit
kleinstmöglichem Radius und kleinstmöglicher Dichte.
Den Radius der optimalen Unterdeckung bezeichnen wir mit 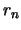 ,
und ihre die Dichte mit
,
und ihre die Dichte mit 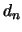 [sie ist klarerweise stets
[sie ist klarerweise stets 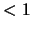 ].
Den Radius der optimalen Überdeckung bezeichnen wir mit
].
Den Radius der optimalen Überdeckung bezeichnen wir mit 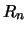 und ihre die Dichte mit
und ihre die Dichte mit 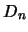 [sie ist klarerweise stets
[sie ist klarerweise stets 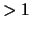 ].
Obwohl die Probleme zueinander dual sind, wurde vor allem das
Unterdeckungsproblem untersucht; auch wir wollen uns vor allem
mit ihm beschäftigen.
Auf einen Zusammenhang des Unterdeckungsproblemes mit Fragen
der Informationstheorie hat v.d. Waerden [95] hingewiesen.
].
Obwohl die Probleme zueinander dual sind, wurde vor allem das
Unterdeckungsproblem untersucht; auch wir wollen uns vor allem
mit ihm beschäftigen.
Auf einen Zusammenhang des Unterdeckungsproblemes mit Fragen
der Informationstheorie hat v.d. Waerden [95] hingewiesen.




Nächste Seite: Aus der Polyedergeometrie
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Lagerungen auf der 3-Sphäre
Inhalt
2004-03-25