Nächste Seite: Reguläre Lagerungen
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Problemstellung und Definitionen
Inhalt
Bevor wir uns mit Lagerungsproblemen befassen können, müssen
wir uns zunächst mit einigen Ergebnissen der Polyedergeometrie
vertraut machen.
Eine Menge heißt konvex, wenn in ihr mit je zwei Punkten
auch stets deren Verbindungsstrecke enthalten ist. Konvexe
Mengen, die kompakt sind und ein nichtleeres Inneres besitzen,
heißen konvexe Körper.
Unter einem konvexen Polytop P verstehen wir einen
Durchschnitt von endlich vielen Halbräumen 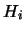 , die bis auf
Permutationen eindeutig bestimmt sind. Es ist dann:
, die bis auf
Permutationen eindeutig bestimmt sind. Es ist dann:
Hat der einbettende Raumes die Dimension 2, so sprechen wir von
Polygonen, hat er die Dimension 3, sprechen wir von
Polyedern.
Zu jedem Polytop gibt es ein duales Polytop. Das zu einem
Polytop 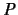 duale Polytop
duale Polytop 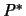 entsteht als
Schnitt der Halbräume
entsteht als
Schnitt der Halbräume
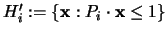 ,
die zu den Ecken von
,
die zu den Ecken von 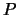 in Bezug auf die Sphäre
in Bezug auf die Sphäre  ' polar' sind:
' polar' sind:
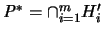 .
Analytisch läßt sich das duale Polytop beschreiben durch:
.
Analytisch läßt sich das duale Polytop beschreiben durch:
Mit
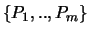 bezeichnen wir hier die Eckpunkte von P;
weiters wird mit
bezeichnen wir hier die Eckpunkte von P;
weiters wird mit 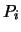 auch der zum Punkt
auch der zum Punkt 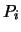 gehörige Ortvektor
bezeichnet.
gehörige Ortvektor
bezeichnet.
Es gilt, daß das duale Polyeder eines Polyeders mit e Ecken
und f Flächen stets ein f-eckiges und e-flächiges Polyeder ist.
Die obige Dualitätsdefinition kann wörtlich auf die Menge 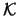 der konvexen Körper übertragen werden. Es sind duale Mengen
konvexer Körper stets wieder konvexe Körper und es gilt [51]:
der konvexen Körper übertragen werden. Es sind duale Mengen
konvexer Körper stets wieder konvexe Körper und es gilt [51]:
Wir betrachten nun eine endliche Anzahl von Halbkugeln auf
der Sphäre. Besitzt ihr Durchschnitt Q innere Punkte, so heißt
Q konvexes sphärisches Vieleck, bzw. konvexes sphärisches
Polygon. Der Flächeninhalt eines konvexen, sphärischen n-Eckes mit
Winkeln
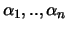 ist gegeben durch
ist gegeben durch
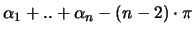 .
Daher ist der Flächeninhalt eines Dreiecks auf der Einheitskugel
mit den Winkeln
.
Daher ist der Flächeninhalt eines Dreiecks auf der Einheitskugel
mit den Winkeln 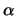 ,
,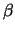 ,
,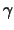 gegeben durch
gegeben durch
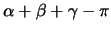 .
Ist ein konvexes Polyeder P des
.
Ist ein konvexes Polyeder P des
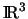 mit
f Flächen, k Kanten und e Ecken gegeben, so
können wir um jeden inneren Punkt
mit
f Flächen, k Kanten und e Ecken gegeben, so
können wir um jeden inneren Punkt 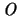 eine Einheitskugel schlagen und die Flächen des Polyeders auf
die Kugeloberfläche projizieren.
So erhalten wir auf der Kugeloberfläche sphärische Vielecke,
die diese schlicht überdecken: jeder Punkt der Sphäre liegt im
Inneren von höchstens einem und in der abgeschlossenen Hülle
von mindestens einem Vieleck dieser Projektion. Eine schlichte
Überdeckung der Kugel durch Polygone heißt auch Mosaik.
Wir wenden nun die obige Flächeninhaltsformel für sphärische
konvexe n-Ecke auf jedes Vieleck der Projektion an und summieren
über alle Vielecke.
eine Einheitskugel schlagen und die Flächen des Polyeders auf
die Kugeloberfläche projizieren.
So erhalten wir auf der Kugeloberfläche sphärische Vielecke,
die diese schlicht überdecken: jeder Punkt der Sphäre liegt im
Inneren von höchstens einem und in der abgeschlossenen Hülle
von mindestens einem Vieleck dieser Projektion. Eine schlichte
Überdeckung der Kugel durch Polygone heißt auch Mosaik.
Wir wenden nun die obige Flächeninhaltsformel für sphärische
konvexe n-Ecke auf jedes Vieleck der Projektion an und summieren
über alle Vielecke.
Da die Kugeloberfläche [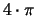 ] gleich groß ist wie die Summe
der Projektionsflächen [das ist
] gleich groß ist wie die Summe
der Projektionsflächen [das ist
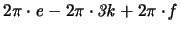 ],
erhalten wir die Euler'sche Polyederformel
],
erhalten wir die Euler'sche Polyederformel
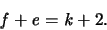 |
(1.1) |
In jedem Polyeder ist
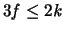 ,
und
,
und
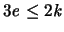 ,
da jede Fläche von mindesten drei Kanten begrenzt ist, und in
jeder Ecke mindestens drei Kanten zusammentreffen. Dabei wird
insgesamt jede Kante doppelt gezählt. Aus der Euler'schen Formel
und aus diesen Ungleichungen folgt:
,
da jede Fläche von mindesten drei Kanten begrenzt ist, und in
jeder Ecke mindestens drei Kanten zusammentreffen. Dabei wird
insgesamt jede Kante doppelt gezählt. Aus der Euler'schen Formel
und aus diesen Ungleichungen folgt:
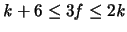 und
und
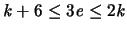 .
Bezeichnet
.
Bezeichnet
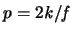 die
mittlere Seitenanzahl einer Fläche und bezeichnet
die
mittlere Seitenanzahl einer Fläche und bezeichnet
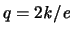 mittlere Kantenanzahl einer Ecke,
so gelten die Ungleichungen:
mittlere Kantenanzahl einer Ecke,
so gelten die Ungleichungen:
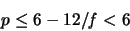 |
(1.2) |
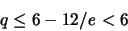 |
(1.3) |
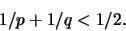 |
(1.4) |
Eine Polyederfläche wollen wir regelmäßig nennen, wenn sie
durch ein reguläres Polygon, d.i. ein Polygon mit gleich großen
Winkeln und gleich großen Seiten, gebildet wird. Eine Ecke
nennen wir regulär, wenn aus einer Kugel um diese Ecke, die
weder auf ihrem Rand noch in ihrem Inneren weitere Polyederecken
enthält, durch die angrenzenden Seitenflächen stets ein
reguläres sphärisches Polygon herausgeschnitten wird.
Besitzt ein Polyeder nur reguläre Ecken und nur reguläre
Flächen , so sprechen wir von einem regulären Polyeder oder
Platonischen Körper. Diesen Körpern schreibt Plato in
seiner ''Ideenlehre'' - als Muster der Vollendung -
besondere Eigenschaften zu.
Da bei ihnen alle Flächen regulär sind, müssen alle Flächen
gleich viele Ecken besitzen; analogerweise treffen sich in
jeder Ecke gleich viele Kanten. Daher wird ein platonischer
Körper, bei dem jede Fläche p die Ecken und jede Ecke q Kanten
besitzt, üblicherweise mit dem Symbol p,q bezeichnet.
Wegen
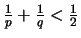 gibt es im
gibt es im
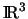 nur folgende reguläre Körper :
nur folgende reguläre Körper :
| reguläres |
Tetraeder |
{3,3} |
| reguläres |
Hexaeder (Würfel) |
{3,4} |
| reguläres |
Ikosaeder |
{3,5} |
| reguläres |
Oktaeder |
{4,3} |
| reguläres |
Pentagon-Dodekaeder |
{5,3} |
Auch die Dualkörper der regulären Körper sind regulär, da
durch die Dualitätstransformation aus regulären Flächen
reguläre Ecken und aus regulären Ecken reguläre Flächen werden.
Es gilt: Das Tetraeder ist sein eigener Dualkörper, der Würfel
ist der Dualkörper der Oktaeders, das Oktaeder ist der
Dualkörper der Würfels, das Ikosaeder ist der Dualkörper des
Pentagon-Dodekadeders und das Pentagon-Dodekaeder ist der Dualkörper
des Ikosaeders.
Als nächste Klasse bieten sich zur Untersuchung die Polyeder
an, die entweder nur reguläre Flächen oder nur reguläre
Ecken besitzen. Von größerem Interesse sind für uns die Polyeder
mit regulären Flächen.
Sind ihre Ecken zueinander kongruent, so heißen sie Archimedische
Körper und werden üblicherweise mit (i,j,k,..) bezeichnet.
Diese Schreibweise besagt, daß in einer Ecke ein i-, dann
ein j-, dann ein k-Eck usw. zusammentreffen. [Die Struktur der
Flächen, die sich um eine Ecke gruppieren, ist überall gleich.]
Die meisten Archimedischen Körper kann man aus den Platonischen
dadurch konstruieren, daß man die Ecken in geeigneter
Weise '' kappt'' . Einen Überblick über die in
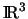 vorhandenen
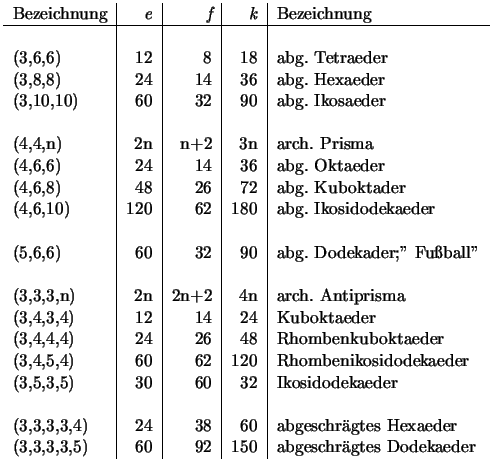
Archimedischen Körper gibt die folgende Tabelle, die nur die 15
nichtentarteten Fälle enthält [30]:
[abg. ='' abgestumpftes '' , arch. = '' archimedisches '']
vorhandenen
Archimedischen Körper gibt die folgende Tabelle, die nur die 15
nichtentarteten Fälle enthält [30]:
[abg. ='' abgestumpftes '' , arch. = '' archimedisches '']
Die Klasse der halbregulären Körper mit regulären Ecken (sie
enthält z.B. das Rhombendodekaeder) entsteht durch
Dualitiätstransformation aus der Klasse der Archimedischen Körper.
Sind auf einer Sphäre n Punkte
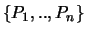 gegeben, so
können wir aus ihnen unter anderem auf folgende zwei Arten
Polyeder konstruieren:
gegeben, so
können wir aus ihnen unter anderem auf folgende zwei Arten
Polyeder konstruieren:




Nächste Seite: Reguläre Lagerungen
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Problemstellung und Definitionen
Inhalt
2004-03-25
![]() gibt es im
gibt es im
![]() nur folgende reguläre Körper :
nur folgende reguläre Körper :