



Nächste Seite: Sphärische Designs
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Kugelkappendiskrepanz, Methode von Beck
Inhalt
Betrachtet man die Definition der Diskrepanzen und die der Gleichverteilung
genauer, so erkennt man, daß das Grundproblem das ist, die Größe
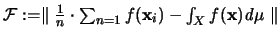 bei festem Maß
bei festem Maß
 im Kompaktum X für eine geeignete Klasse
im Kompaktum X für eine geeignete Klasse  von Funktionen
von Funktionen  und für eine geeignete Norm möglichst klein zu machen.
Klarerweise ist unser Kompaktum stets die
und für eine geeignete Norm möglichst klein zu machen.
Klarerweise ist unser Kompaktum stets die  mit dem
Oberflächenmaß
mit dem
Oberflächenmaß 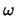 , bzw. mit dem normierten Oberflächenmaß
, bzw. mit dem normierten Oberflächenmaß 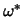
Verwendet man die Maximumsnorm und die Klasse der
Indikatorfunktionen der sphärischen Kugelkappen auf  ,
so erhält man die Kugelkappendiskrepanz aus Paragraph 2.
,
so erhält man die Kugelkappendiskrepanz aus Paragraph 2.
In diesem Paragraphen wird die Operatordiskrepanz betrachtet,
die entsteht, wenn der Fehler 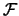 in der
in der 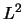 -Norm für die Funktionen
der Klasse
-Norm für die Funktionen
der Klasse
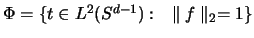 möglichst gering werden soll.
möglichst gering werden soll.
Die hier vorgestellte Methode, die auch bei anderen
Diskrepanzen verwendet werden kann, ist konstruktiv, liefert aber
schwächere Ergebnisse als die Methoden von Beck.
Wir wollen uns daher mit einer Skizze begnügen; die genaue
Beschreibung findet man in [57] und [58].
Die Methode sucht nicht nach Punkten auf der Kugel,
sondern nach Rotationen der Kugel. Klarerweise wird dann durch die
Drehachsen eine Menge von Punkten auf der Kugel erzeugt.
Es sei G stets die SO(3), das ist die Gruppe aller
Rotationen im 3-dimensionalen Raum. Wir entnehmen G eine
symmetrische und gleichverteilte Folge von Rotationen. Dabei wird
''gleichverteilt'' im üblichen Sinn gebraucht, und unter
''symmetrisch'' verstehen wir, daß die Folge mit jeder Rotation
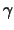 auch die inverse Rotation
auch die inverse Rotation 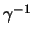 enthält.
enthält.
Ist eine derartige Folge
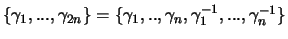 gegeben,
so definieren wir uns für alle
gegeben,
so definieren wir uns für alle
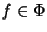 den Heckeoperator
den Heckeoperator
Es sei nun:
und für die Folge
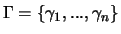 sei
sei
Dann verstehen unter
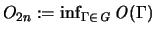 die Operatordiskrepanz, wobei wir das Infimum über alle möglichen
Folgen
die Operatordiskrepanz, wobei wir das Infimum über alle möglichen
Folgen 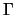 bilden.
bilden.
Wie die Autoren in [57] aufzeigen, ist läßt der Hecke-Operator,
der die Operatornorm
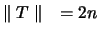 hat, jeden Raum der
sphärischen harmonischen Spektralanalyse invariant.
hat, jeden Raum der
sphärischen harmonischen Spektralanalyse invariant.
Der Raum 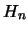 der sphärischen harmonischen Spektralanalyse der
Ordnung n ist definiert als der Eigenraum des Laplace-Operators
der sphärischen harmonischen Spektralanalyse der
Ordnung n ist definiert als der Eigenraum des Laplace-Operators
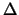 zu dem Eigenwert
zu dem Eigenwert 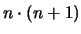 und hat die Dimension
und hat die Dimension 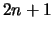 ; der
Laplace-Operator
; der
Laplace-Operator 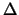 ( s.S.58) zerlegt den
( s.S.58) zerlegt den 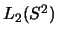 -Raum in die
direkte Summe der
-Raum in die
direkte Summe der 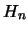 [57, 67].
[57, 67].
Die Legendre-Polynome 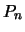 werden erzeugt durch die Gleichung:
werden erzeugt durch die Gleichung:
Sie bilden eine wichtige Funktionenfamilie der Räume 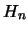 und
sind zueinander orthogonal.
und
sind zueinander orthogonal.
Weiters gibt es eine Orthonormalbasis
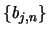 von
von 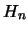 , die den
Heckeoperator T diagonalisiert [57]. Ist
, die den
Heckeoperator T diagonalisiert [57]. Ist 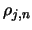 der zum
Basiselement
der zum
Basiselement
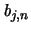 zugehörigen Eigenwert, so gilt:
zugehörigen Eigenwert, so gilt:
Dann ist Spur von
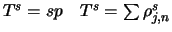 (mit Summe über
(mit Summe über
 ).
).
Bezeichnet 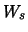 die Menge aller ''Wörter der Länge s'' in
die Menge aller ''Wörter der Länge s'' in
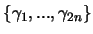 , so kann
, so kann 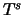 auch geschrieben werden als
auch geschrieben werden als
 .
Diese Summe ist gleich
.
Diese Summe ist gleich
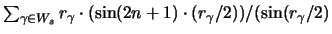 , wo
, wo
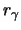 den Drehwinkel der Rotation
den Drehwinkel der Rotation 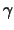 bezeichnet.
Ist
bezeichnet.
Ist 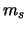 die Anzahl aller Wörter der Länge s, die die Identität
buchstabieren, so folgt, da
die Anzahl aller Wörter der Länge s, die die Identität
buchstabieren, so folgt, da
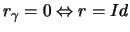 , [57] :
, [57] :
Diese Grenzwertbeziehung ermutigt, durch
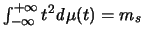 für
für 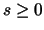 ein Wahrscheinlichkeitsmaß zu definieren.
ein Wahrscheinlichkeitsmaß zu definieren.
Bezeichnet 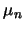 das Spektralmaß von
das Spektralmaß von 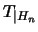 , so wird durch die
angegebene Grenzwertbeziehung die Konvergenz der Maße in der
schwach-*-Topologie aufgezeigt; d.h.: für jede stetige Funktion
, so wird durch die
angegebene Grenzwertbeziehung die Konvergenz der Maße in der
schwach-*-Topologie aufgezeigt; d.h.: für jede stetige Funktion 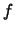 gilt:
gilt:
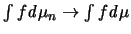
Das Spektralmaß ist das Maß, das jedem Eigenwert eines
Operators die Masse 1/(Dimension des Raumes) zuordnet; dabei
werden die Eigenwerte gemäß ihrer Vielfachheit gezählt.
Daher gibt 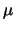 den Ort an, an dem der Großteil des Spektrums
[=Großteil der ''Masse''] von T zu finden ist. Speziell besteht
der Träger von
den Ort an, an dem der Großteil des Spektrums
[=Großteil der ''Masse''] von T zu finden ist. Speziell besteht
der Träger von 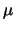 (:=
(:=
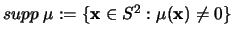 )
aus Grenzwerten der Eigenwerte von T.
)
aus Grenzwerten der Eigenwerte von T.
Weiters wird das Maß 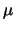 allein durch die natürliche Zahl
allein durch die natürliche Zahl 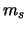 definiert
und hängt daher nur von der durch
definiert
und hängt daher nur von der durch
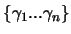 erzeugten
Gruppe
erzeugten
Gruppe 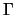 ab. Aus diesem Grund kann das Maß
ab. Aus diesem Grund kann das Maß 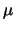 auch als Markovkette
auf
auch als Markovkette
auf 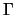 interpretiert werden [57].
interpretiert werden [57].
Damit die Markovkette translationsinvariant wird und das
Spektralmaß 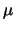 besitzt, muß die Wahrscheinlichkeit, von
besitzt, muß die Wahrscheinlichkeit, von
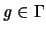 nach
nach
![$\gamma_i {\mathit g} [\in \Gamma]$](img442.gif) zu kommen,
überall gleich 1/2n sein [57].
zu kommen,
überall gleich 1/2n sein [57].
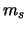 entpuppt sich in dieser Uminterpretation als die Anzahl
der Wege der Länge s, die von einem Punkt g ausgehend zum
selben Punkt g zurückführen.
entpuppt sich in dieser Uminterpretation als die Anzahl
der Wege der Länge s, die von einem Punkt g ausgehend zum
selben Punkt g zurückführen.
Eine derartige Markovkette wurde von Kesten [46] untersucht.
Er bewies, daß unter gewissen Bedingung das größte Trägerelement
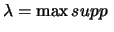 mu
mu
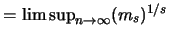 von
von 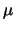 gleich 2n ist und sonst stets
gleich 2n ist und sonst stets
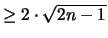 ausfällt.
ausfällt.
Die gesuchte Diskrepanz 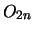 ist gleich dem zweitgrößten
Eigenwert von T/2n [57]. Aus dem Satz von Kesten folgt daher:
ist gleich dem zweitgrößten
Eigenwert von T/2n [57]. Aus dem Satz von Kesten folgt daher:
In umgekehrter Richtung gilt:
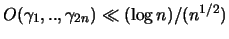 .
.
Ein Zusammenhang zwischen 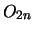 und T/2n wird bereits deutlich,
wenn man die Norm
und T/2n wird bereits deutlich,
wenn man die Norm
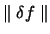 betrachtet:
betrachtet:
Es wird in [58] auch gezeigt, daß man für jede Primzahl p mit
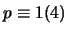 eine Menge
eine Menge
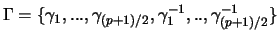 finden kann,
für die
finden kann,
für die
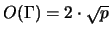 ist.
ist.
Die zitierten Artikel enthalten auch Computerprogramme, mit
denen optimale Rotationsanordnungen berechnet werden können.
Tabellarische und, für spezielle Werte, auch graphische
Ausdrucke geben einen Überblick über die optimalen Anordnungen.
Für die sphärische Kappendiskrepanz und die Diskrepanz des
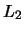 -Mittels gilt:
-Mittels gilt:
Es sei:
Dann ist:
-
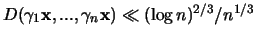
-
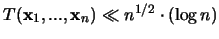 .
.
Die vergleichbaren Beck'schen Resultate lauten:
-
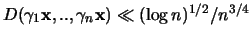
-
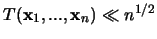 ,
,
sind also durchwegs schärfer, aber nicht konstruktiv.
Ein merkwürdiger Satz über die Verteilung von Punkten auf
der 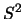 , ist folgender [25]:
, ist folgender [25]:
Es gibt zwei Konstante 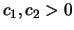 , sodaß es
, sodaß es
(i) für jede natürliche Zahl n und für jedes 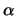 mit
mit
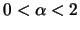 eine Anordnung von n Punkten auf
eine Anordnung von n Punkten auf 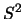 gibt,
in der jeder Punkt von mindestens
gibt,
in der jeder Punkt von mindestens
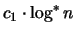 anderen
Distanz
anderen
Distanz 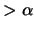 hat, und daß es
hat, und daß es
(ii) für jede natürliche Zahl n eine Anordnung von n Punkten
auf 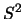 gibt, in der jeder Punkt von mindestens
gibt, in der jeder Punkt von mindestens
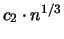 anderen
Punkten Abstand
anderen
Punkten Abstand 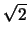 hat.
hat.
[Haben zwei Punkte auf der  den Abstand
den Abstand 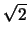 , so stehen die
zugehörigen Ortvektoren orthogonal aufeinander.]
, so stehen die
zugehörigen Ortvektoren orthogonal aufeinander.]
Mit 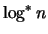 wird dabei die kleinste natürliche Zahl r
bezeichnet, sodaß man, bei Start in n, die log-Funktion r-mal
iterieren muß, um einen Wert
wird dabei die kleinste natürliche Zahl r
bezeichnet, sodaß man, bei Start in n, die log-Funktion r-mal
iterieren muß, um einen Wert 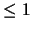 zu erhalten.
zu erhalten.
Bezeichnen wir mit 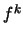 die k-te Iteration der Funktion f, so ist also
die k-te Iteration der Funktion f, so ist also
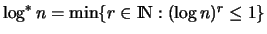 . Diese Funktion ist
Null für n = 1; für
. Diese Funktion ist
Null für n = 1; für
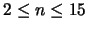 ist ihr Wert gleich 2; den Wert
3 nimmt sie an für
ist ihr Wert gleich 2; den Wert
3 nimmt sie an für
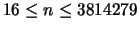 , usw.
, usw.
Die Beweisidee für (i) ist folgende :
Wir fixieren uns ein 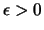 , sodaß der Durchmesser eines
Breitenkreises vom Abstand
, sodaß der Durchmesser eines
Breitenkreises vom Abstand 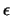 von der Äquatorebene stets
größer
von der Äquatorebene stets
größer 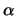 ist [
ist [
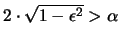 ].
Die beiden Breitenkreise, die von der Äquatorebene
den Abstand
].
Die beiden Breitenkreise, die von der Äquatorebene
den Abstand 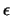 haben, begrenzen dann einen Parallelstreifen
haben, begrenzen dann einen Parallelstreifen
Für jedes 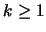 wird nun eine Punktmenge
wird nun eine Punktmenge 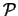 konstruiert, in der
jeder Punkt von zumindest k anderen Abstand
konstruiert, in der
jeder Punkt von zumindest k anderen Abstand 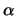 besitzt.
besitzt.
Es sei für ein natürliches k eine derartige Menge
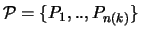 gegeben, die sich zudem in einem kleinen
gegeben, die sich zudem in einem kleinen
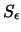 -Streifen [
-Streifen [
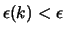 ] um den Äquator befinde.
(für k=1 bestehe
] um den Äquator befinde.
(für k=1 bestehe 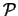 aus zwei Punkten mit Abstand
aus zwei Punkten mit Abstand 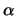 auf dem
Äquator.)
Es sei U ein Punkt in der Nähe des Nordpols, von dem er den
(beliebig) kleinen Abstand
auf dem
Äquator.)
Es sei U ein Punkt in der Nähe des Nordpols, von dem er den
(beliebig) kleinen Abstand 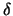 habe.
habe.
Wir lassen die Punktmenge 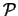 um die Achse -UU rotieren. Die
Kugel wird dabei so um die Achse -UU gedreht, daß der Punkt
um die Achse -UU rotieren. Die
Kugel wird dabei so um die Achse -UU gedreht, daß der Punkt 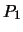 auf einen Punkt
auf einen Punkt 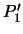 , der von
, der von 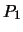 den Abstand
den Abstand
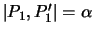 besitzt, abgebildet wird. Diese Rotation
bezeichen wir mit
besitzt, abgebildet wird. Diese Rotation
bezeichen wir mit 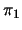 . Analog dazu sei
. Analog dazu sei 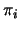 die Drehung um -UU,
die
die Drehung um -UU,
die 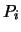 auf
auf 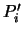 überführt. Auch hier sei
überführt. Auch hier sei
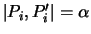 .
Es sei
.
Es sei
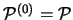 ,
,
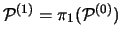 . Sind die Mengen
. Sind die Mengen
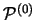 ,
,
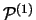 ,...,
,...,
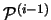 bereits vorhanden, so wird
bereits vorhanden, so wird
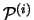 definiert durch [
definiert durch [
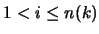 ]:
]:
Die so erhaltenen Mengen werden zuletzt noch in
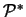 vereinigt:
vereinigt:
Entscheidend für diese rekursive Konstruktion ist eine gute
Wahl der Achse -UU. Mit einer geeigneten Wahl kann man nämlich
erreichen, daß alle Drehungen 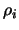 existieren, daß die Mengen
existieren, daß die Mengen
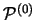 ,
,
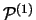 ,...,
,...,
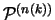 paarweise disjunkt sind,
und daß sich die Menge
paarweise disjunkt sind,
und daß sich die Menge
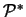 auf einem
auf einem
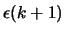 -Streifen
mit
-Streifen
mit
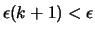 um den Äquator befinden.
um den Äquator befinden.
Aufgrund unserer Rekursion ist
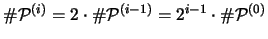 ,
da bei Bildung von
,
da bei Bildung von
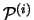 jeder Punkt von
jeder Punkt von
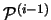 einen Bildpunkt
[
einen Bildpunkt
[
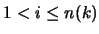 ] erhält.
Da alle Mengen paarweise disjunkt sind, enthält die Vereinigung von
] erhält.
Da alle Mengen paarweise disjunkt sind, enthält die Vereinigung von
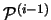 und
und
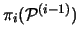 genau
genau
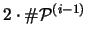 Punkte.
Punkte. Setzen wir
Punkte.
Punkte. Setzen wir
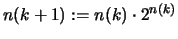 , so ist:
, so ist:
also
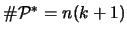 .
Es ist
.
Es ist
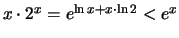 ist für
ist für 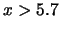 .
Daher können wir mit vollständiger Induktion zeigen, daß gilt:
.
Daher können wir mit vollständiger Induktion zeigen, daß gilt:
Denn : 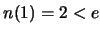 ;
;
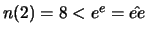 (Dabei sei
(Dabei sei 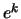 die k-fache Potenz von e:
die k-fache Potenz von e:
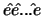 )
)
Ist
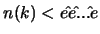 (k mal), so ist:
(k mal), so ist:
In der Menge
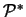 hat jeder Punkt von mindesten (k+1) anderen
genau den Abstand
hat jeder Punkt von mindesten (k+1) anderen
genau den Abstand 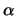 , wie man durch Nachrechnen beweist.
, wie man durch Nachrechnen beweist.
Der Beweis der zweiten Aussage stützt sich auf einen analogen
Satz der Ebene, dessen Konstruktion auf die Sphäre übertragen
wird.




Nächste Seite: Sphärische Designs
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Kugelkappendiskrepanz, Methode von Beck
Inhalt
2004-03-25
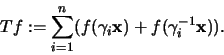
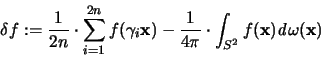
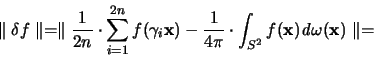
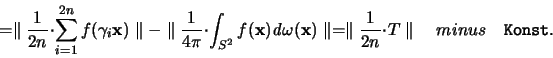
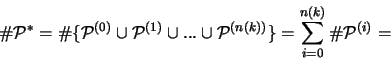
![\begin{displaymath}
\char93 {\mathcal P}^{(0)} + \sum_{i=0}^{n(k)} (2^{i-1} \cd...
...=
\char93 {\mathcal P}^{(0)} \cdot [1+2^{n(k)}-1] = n(k+1),
\end{displaymath}](img507.gif)