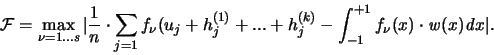Nächste Seite: Invarianzprinzip
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Rotationen und Operatordiskrepanz
Inhalt
Wie bereits bemerkt wurde (2.4), besteht ein Zusammenhang
zwischen der Diskrepanztheorie und der numerischen Integration.
In der Numerik will man vor allem die Polynome, die
' Grundbausteine' der Funktionen, exakt zu berechnen. Daher
sucht man üblicherweise nach Stützpunkten, bei denen der Fehler
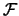 genau dann Null wird, wenn P ein Polynom ist.
genau dann Null wird, wenn P ein Polynom ist.
Eine Menge
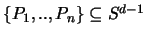 soll daher
d-dimensionales sphärisches t-Design (
soll daher
d-dimensionales sphärisches t-Design (
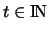 ) heißen,
wenn für jedes Polynom P mit Grad
) heißen,
wenn für jedes Polynom P mit Grad 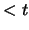 gilt:
gilt:
Die Existenz sphärischer Designs wurde erst 1984 in [77]
nachgewiesen. In [23] und in [33] wird gezeigt, daß für ein
festes t die Anzahl der Punkte, für die ein sphärisches Design
existiert, eine untere Schranke von der Größenordnung 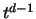 besitzt. Weiters sei erwähnt, daß die Ecken eines Fußballes
kein Design bilden [34].
besitzt. Weiters sei erwähnt, daß die Ecken eines Fußballes
kein Design bilden [34].
Wir wollen jetzt ansatzweise die Existenz eines sphärischen
t-Designs für
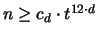 beweisen [98]. Weiters
wollen wir zeigen, daß auch für rechteckige Bereiche der
beweisen [98]. Weiters
wollen wir zeigen, daß auch für rechteckige Bereiche der  Designs
existieren ( s.[99],Lemma 3).
Diese Aussagen sind Korollare zu folgendem Satz der
numerischen Integration [98],[99]:
Designs
existieren ( s.[99],Lemma 3).
Diese Aussagen sind Korollare zu folgendem Satz der
numerischen Integration [98],[99]:
Es sei 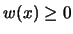 eine auf [-1,+1] definierte und integrable
Gewichtsfunktion für die mit
eine auf [-1,+1] definierte und integrable
Gewichtsfunktion für die mit
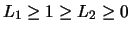 und
und
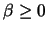 gilt:
gilt:
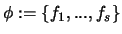 sei eine Klasse 3-mal stetig differentierbarer
Funktionen auf [-1,+1], deren erste Ableitungen in Bezug zur
Gewichtsfunktion w orthogonal sind. Das heißt:
sei eine Klasse 3-mal stetig differentierbarer
Funktionen auf [-1,+1], deren erste Ableitungen in Bezug zur
Gewichtsfunktion w orthogonal sind. Das heißt:
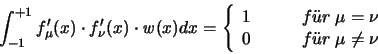 |
(2.14) |
Es sei für die Funktionen dieser Klasse:
sowie
Dann gilt:
(a) Für
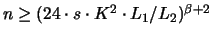 bzw.
bzw.
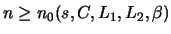 gibt
es Punkte
gibt
es Punkte
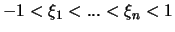 , sodaß für alle
, sodaß für alle 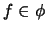 gilt:
gilt:
(b) Es werde 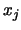 definiert durch die Gleichung:
definiert durch die Gleichung:
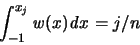 |
(2.15) |
Dann können wir annehmen, daß
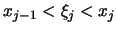 und daß gilt:
und daß gilt:
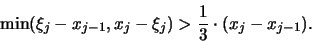 |
(2.16) |
Um die gewünschten Korollare zu erhalten, betrachten wir das Polynom
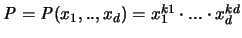 mit
mit 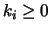 und
und
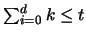 .
.
Führen wir in der üblichen Weise Polarkoordinaten ein, und
setzen wir
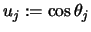 , so gilt:
, so gilt:
mit
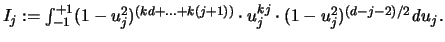
Die Anwendung des Satzes auf die spezielle Klasse der
Gegenbauerpolynome ergibt, daß es für jede Koordinate 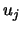 eine Menge
eine Menge
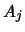 gibt, für die das Integral
gibt, für die das Integral 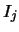 durch eine Summe ersetzt
werden kann [98].
durch eine Summe ersetzt
werden kann [98].
Es sei
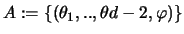 die Menge der Punkte aus
die Menge der Punkte aus
 , die entsteht, wenn
, die entsteht, wenn 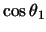 ,...,
,...,
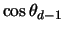 und
und
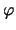 unabhängig
voneinander die Mengen
unabhängig
voneinander die Mengen
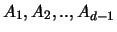 durchlaufen. A ist dann ein
sphärisches Design der Ordnung t. Daß dazu notwendigerweise
durchlaufen. A ist dann ein
sphärisches Design der Ordnung t. Daß dazu notwendigerweise
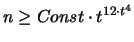 sein muß, wird in [98] bewiesen.
Auch die zweite Aussage kann man als Folgerung des Satzes
beweisen [99]. Auch hier muß man man den Satz auf eine spezielle
Funktionenklasse
sein muß, wird in [98] bewiesen.
Auch die zweite Aussage kann man als Folgerung des Satzes
beweisen [99]. Auch hier muß man man den Satz auf eine spezielle
Funktionenklasse  anwenden.
anwenden.
Durch die Gleichungen
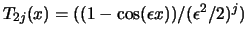
und
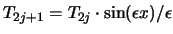
.
erhält man eine Menge
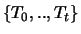 von Funktionen. Um
von Funktionen. Um 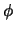 zu
erhalten muß man nur noch diese Menge orthogonalisieren. Dabei
ist
zu
erhalten muß man nur noch diese Menge orthogonalisieren. Dabei
ist 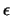 ein positiver reeller Parameter.
ein positiver reeller Parameter.
Es sei
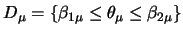 ein rechteckiger Bereich auf
ein rechteckiger Bereich auf  . Da man ein größeres Gebiet stets
in mehrere Teilgebiete zerlegen kann, können wie den Bereich D als
genügend klein annehmen. Dann kann man mit ähnlichen Methoden beweisen,
daß es
für jeden Bereich
. Da man ein größeres Gebiet stets
in mehrere Teilgebiete zerlegen kann, können wie den Bereich D als
genügend klein annehmen. Dann kann man mit ähnlichen Methoden beweisen,
daß es
für jeden Bereich
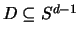 dieser Gestalt eine
von D unabhängige, natürliche Zahl
dieser Gestalt eine
von D unabhängige, natürliche Zahl 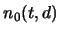 gibt, sodaß es für jedes
(d-1)-Tupel natürlicher Zahlen
gibt, sodaß es für jedes
(d-1)-Tupel natürlicher Zahlen
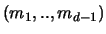 mit
mit 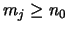 eine Menge von
eine Menge von
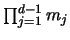 Punkten aus D gibt, die
ein sphärisches Design der Ordnung t bildet [98].
Punkten aus D gibt, die
ein sphärisches Design der Ordnung t bildet [98].
Für den Satz selbst soll nun eine Beweisskizze folgen. Die
exakte Ausführung des Beweises findet sich in [98].
Wir starten bei der natürlichen Annahme, daß die Menge der
Interpolationspunkte
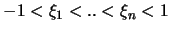 eine Verteilung
besitzt, die zu der durch die Gewichtsfunktion w induzierten
Verteilung ''nahe'' steht, und verwenden dann die folgenden
drei Schritte:
eine Verteilung
besitzt, die zu der durch die Gewichtsfunktion w induzierten
Verteilung ''nahe'' steht, und verwenden dann die folgenden
drei Schritte:
(1) Wir zerlegen das Intervall [-1,+1] in n Teilintervalle
![$I_1=[x_0,x_1]$](img567.gif) ,
, ![$I_1=[x_1,x_2]$](img568.gif) ,...,
,...,
![$I_n = [x_{n-1},x_n]$](img569.gif) von gleicher
w-Länge. Das bedeutet, daß
von gleicher
w-Länge. Das bedeutet, daß
sein soll. Klarerweise ist 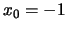 und
und 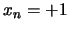 zu setzen.
zu setzen.
Im Inneren eines jeden Intervalles 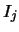 wählen wir den
eindeutig bestimmten Punkt
wählen wir den
eindeutig bestimmten Punkt 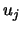 , für den gilt:
, für den gilt:
(2) Die Menge
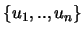 benützen wir als Startmenge eines
Newton'schen Iterationsprozesses. Das bedeutet, daß die Punkte
benützen wir als Startmenge eines
Newton'schen Iterationsprozesses. Das bedeutet, daß die Punkte
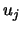 sukzessive durch die besser approximierenden Punkte
sukzessive durch die besser approximierenden Punkte
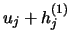
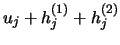 .. ersetzt werden.
Die Korrekturglieder
.. ersetzt werden.
Die Korrekturglieder 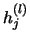 können [98] mittels Lagrangemethode
so gewählt werden, daß
können [98] mittels Lagrangemethode
so gewählt werden, daß
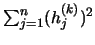 minimal wird.
Dabei ist die geforderte w-Orthogonalität nötig, um die auftretenden
Korrekturglieder klein halten zu können.
minimal wird.
Dabei ist die geforderte w-Orthogonalität nötig, um die auftretenden
Korrekturglieder klein halten zu können.
(3) Die Iterationsprozedur erzeugt rekursive Ungleichungen
für die Korrekturglieder 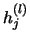 und für den Fehler
und für den Fehler
Da für hinreichend große n der Fehler 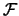 mit wachsendem k nach
Null strebt, und da die Grenzpunkte
mit wachsendem k nach
Null strebt, und da die Grenzpunkte
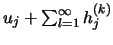 existieren, paarweise disjunkt sind und in [-1,+1] liegen, können
wir den Beweis schließen.
existieren, paarweise disjunkt sind und in [-1,+1] liegen, können
wir den Beweis schließen. 




Nächste Seite: Invarianzprinzip
Aufwärts: Diskrepanzen auf der Kugel
Vorherige Seite: Rotationen und Operatordiskrepanz
Inhalt
2004-03-25
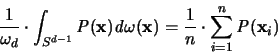
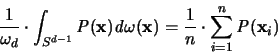
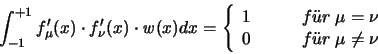
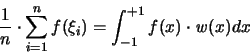
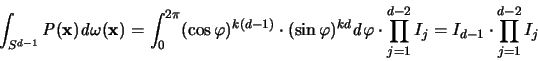
![]() eine Menge
eine Menge
![]() gibt, für die das Integral
gibt, für die das Integral ![]() durch eine Summe ersetzt
werden kann [98].
durch eine Summe ersetzt
werden kann [98].
![]() die Menge der Punkte aus
die Menge der Punkte aus
![]() , die entsteht, wenn
, die entsteht, wenn ![]() ,...,
,...,
![]() und
und
![]() unabhängig
voneinander die Mengen
unabhängig
voneinander die Mengen
![]() durchlaufen. A ist dann ein
sphärisches Design der Ordnung t. Daß dazu notwendigerweise
durchlaufen. A ist dann ein
sphärisches Design der Ordnung t. Daß dazu notwendigerweise
![]() sein muß, wird in [98] bewiesen.
Auch die zweite Aussage kann man als Folgerung des Satzes
beweisen [99]. Auch hier muß man man den Satz auf eine spezielle
Funktionenklasse
sein muß, wird in [98] bewiesen.
Auch die zweite Aussage kann man als Folgerung des Satzes
beweisen [99]. Auch hier muß man man den Satz auf eine spezielle
Funktionenklasse ![]() anwenden.
anwenden.
![]() ein rechteckiger Bereich auf
ein rechteckiger Bereich auf ![]() . Da man ein größeres Gebiet stets
in mehrere Teilgebiete zerlegen kann, können wie den Bereich D als
genügend klein annehmen. Dann kann man mit ähnlichen Methoden beweisen,
daß es
für jeden Bereich
. Da man ein größeres Gebiet stets
in mehrere Teilgebiete zerlegen kann, können wie den Bereich D als
genügend klein annehmen. Dann kann man mit ähnlichen Methoden beweisen,
daß es
für jeden Bereich
![]() dieser Gestalt eine
von D unabhängige, natürliche Zahl
dieser Gestalt eine
von D unabhängige, natürliche Zahl ![]() gibt, sodaß es für jedes
(d-1)-Tupel natürlicher Zahlen
gibt, sodaß es für jedes
(d-1)-Tupel natürlicher Zahlen
![]() mit
mit ![]() eine Menge von
eine Menge von
![]() Punkten aus D gibt, die
ein sphärisches Design der Ordnung t bildet [98].
Punkten aus D gibt, die
ein sphärisches Design der Ordnung t bildet [98].
![]() eine Verteilung
besitzt, die zu der durch die Gewichtsfunktion w induzierten
Verteilung ''nahe'' steht, und verwenden dann die folgenden
drei Schritte:
eine Verteilung
besitzt, die zu der durch die Gewichtsfunktion w induzierten
Verteilung ''nahe'' steht, und verwenden dann die folgenden
drei Schritte:
![]() ,
, ![]() ,...,
,...,
![]() von gleicher
w-Länge. Das bedeutet, daß
von gleicher
w-Länge. Das bedeutet, daß