



Nächste Seite: Zufallspolyeder
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Einige Maßzahlen konvexer Körper
Inhalt
Will man den ''Abstand'' zweier konvexer Körper untersuchen,
so muß man sich zunächst Gedanken darüber machen, wie dieser
Abstand überhaupt gemessen werden kann, denn auf der Menge 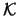 der konvexen Körper gibt es keine ausgezeichnete Metrik.
der konvexen Körper gibt es keine ausgezeichnete Metrik.
Die gebräuchlichste Metrik ist die Hausdorffmetrik, die wir
stets mit 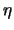 bezeichnen wollen. Sie ist definiert als das
Minimum der Zahlen
bezeichnen wollen. Sie ist definiert als das
Minimum der Zahlen 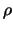 , für die gilt:
, für die gilt:
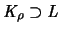 und
und
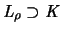 , wobei wir
mit K und L zwei konvexe Körper bezeichnen.
Der Hausdorffabstand
, wobei wir
mit K und L zwei konvexe Körper bezeichnen.
Der Hausdorffabstand
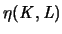 läßt sich auch anschreiben durch:
läßt sich auch anschreiben durch:
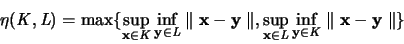 |
(3.9) |
Man kann klarerweise nicht nur das Maximum der beiden Zahlen
in der Klammer zu betrachten, sondern auch deren Mittel. Diese
Mittel führen bei geeigneter Wahl der Gewichtung zu Metriken,
die einen engen Bezug zu den 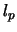 -Metriken haben [38].
-Metriken haben [38].
Mehr Verwendung als derartige Metriken findet jedoch die
Symmetrische Differenzmetrik, die für zwei konvexe Körper
K und L so definiert ist:
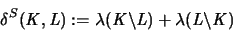 |
(3.10) |
Dabei bezeichnen wir mit 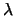 das Lebesguemaß des umgebenden
das Lebesguemaß des umgebenden
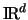 .
[Im folgenden wollen wir stets die Hausdorffmetrik verwenden,
da in dieser Metrik die meisten Ergebnisse vorliegen.]
.
[Im folgenden wollen wir stets die Hausdorffmetrik verwenden,
da in dieser Metrik die meisten Ergebnisse vorliegen.]
Wenn wir konvexe Körper durch konvexe Polyeder approximieren wollen,
sind folgende Sätze wichtig [40]:
Um den ersten Satz zu beweisen, überdecken wir K durch
endlich viele Würfel der Kantenlänge
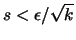 , von denen jeder
Punkte mit K gemeinsam habe und die zB. durch ein achsparalleles
Raster mit Maschen der Länge s gegeben sind.
Es sei Q die konvexe Hülle der Vereinigung dieser Würfel.
Dann ist
, von denen jeder
Punkte mit K gemeinsam habe und die zB. durch ein achsparalleles
Raster mit Maschen der Länge s gegeben sind.
Es sei Q die konvexe Hülle der Vereinigung dieser Würfel.
Dann ist
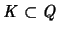 und
und
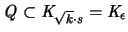 ,
und daher
,
und daher
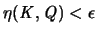 .
.
Weiters überdecken wir K durch endlich viele Würfel der
Kantenlänge
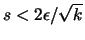 , deren Mittelpunkte alle zu
K gehören sollen. Auch hier wäre an ein Raster denkbar, allerdings sind
eventuell Verschiebungen der einen oder anderen Rasterebene
nötig, um die erforderlichen Bedingung erfüllen zu können.
Nun sei P die konvexe Hülle der Würfelmittelpunkte. Dann ist
, deren Mittelpunkte alle zu
K gehören sollen. Auch hier wäre an ein Raster denkbar, allerdings sind
eventuell Verschiebungen der einen oder anderen Rasterebene
nötig, um die erforderlichen Bedingung erfüllen zu können.
Nun sei P die konvexe Hülle der Würfelmittelpunkte. Dann ist
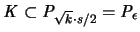 und
und
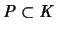 und damit
und damit
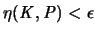
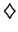
Für den Beweis der zweiten Aussage wählen wir den Ursprung 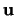 des umgebenden Raumes im Inneren von K, und zwar so, daß eine
Kugel
des umgebenden Raumes im Inneren von K, und zwar so, daß eine
Kugel 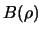 mit Radius
mit Radius 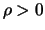 um
um 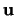 ebenfalls noch ganz im Inneren
von K liegt. Es sei
ebenfalls noch ganz im Inneren
von K liegt. Es sei
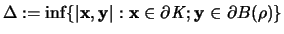 der positive Abstand zwischen den
Rändern dieser Körper.
der positive Abstand zwischen den
Rändern dieser Körper.
Es sei 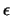 mit
mit
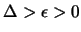 und
und
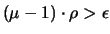 gegeben. Wegen
gegeben. Wegen
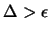 ist
ist
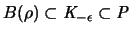 .
Es wäre sogar noch eine Parallelkugel mit
Abstand
.
Es wäre sogar noch eine Parallelkugel mit
Abstand 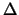 in K enthalten. Allerdings würde
in K enthalten. Allerdings würde
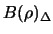 den Körper K in (mindestens) einem Punkt berühren.
den Körper K in (mindestens) einem Punkt berühren.
Gemäß (3.11) gibt es stets ein Polyeder P mit
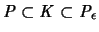 .
Wird dieses Polyeder um den Faktor
.
Wird dieses Polyeder um den Faktor 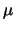 gestreckt, so werden die
Trägerhyperebenen der Seitenflächen, die einen Abstand
gestreckt, so werden die
Trägerhyperebenen der Seitenflächen, die einen Abstand 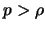 zum Ursprung haben, um die Länge
zum Ursprung haben, um die Länge
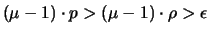 nach
außen verschoben. Daraus folgt:
nach
außen verschoben. Daraus folgt:
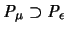
Wir betrachten wir nun die Approximation der 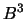 :
:
Es sei zunächst bemerkt, daß sich (I.3.8) und (I.3.10) in folgende Form
bringen lassen [30]:
Ist ein Polyeder mit n Ecken oder n Flächen in eine konzentrische
Kugelschale mit Umkugelradius R und Inkugelradius r eingebettet,
so gilt mit der Konvention
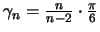 :
:
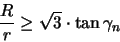 |
(3.12) |
Denn jede Überdeckung definiert ein Polyeder:
Man betrachte den Schnitt der Halbräume, die durch die Trägerhyperebenen
der Kugelkappen begrenzt sind. Das sind die Hyperebenen, die die
Kugelkappen von der Kugel trennen, und die den
Kugelmittelpunkt in ihrem Inneren enthalten.
Besitzt ein Polyeder P von der Einheitskugel 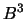 den
Hausdorffabstand
den
Hausdorffabstand 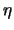 , so ist aufgrund der Definition der Hausdorffmetrik
[
, so ist aufgrund der Definition der Hausdorffmetrik
[
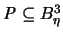 ] das Polyeder in einer Kugel vom
Radius
] das Polyeder in einer Kugel vom
Radius 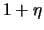 enthalten und enthält [wegen
enthalten und enthält [wegen
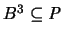 ]
eine Kugel vom Radius
]
eine Kugel vom Radius 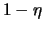 .
.
Das heißt, daß die Abweichung eines n-eckigen oder n-flächigen
Polyeders 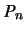 von der Einheitskugel wegen
von der Einheitskugel wegen
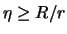 stets die Ungleichung erfüllt:
stets die Ungleichung erfüllt:
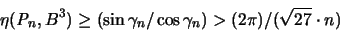 |
(3.13) |
Die Ungleichungen (4) und (5) lassen sich verschärfen [30],
woraus man folgende Korollare erhält:
-
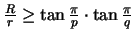 mit
mit
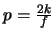 und
und
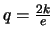 .
.
- Enthält ein n-seitiges Polyeder
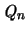 die Einheitskugel, so gilt :
die Einheitskugel, so gilt :
- Enthält ein n-eckiges Polyeder
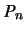 die Einheitskugel, so gilt :
die Einheitskugel, so gilt :
- Ist ein n-eckiges Polyeder
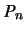 in der Einheitskugel so gilt :
in der Einheitskugel so gilt :




Nächste Seite: Zufallspolyeder
Aufwärts: Approximation der Kugel durch
Vorherige Seite: Einige Maßzahlen konvexer Körper
Inhalt
2004-03-25
![]() :
:
![]() :
: