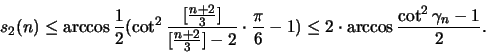Nächste Seite: Halbreguläre Lagerungen
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Aus der Polyedergeometrie
Inhalt
Wir beginnen nun mit der Untersuchung des
Lagerungsproblems und führen dazu folgende Bezeichnungen ein:
Eine Unterdeckung vom Radius r soll r-gesättigt heißen, wenn
man einen weiteren Kreis vom Radius r nur dadurch unterbringen
kann, daß man ihn mit einem bereits vorhandenen schneidet.
Da wir eine nicht gesättigte Unterdeckung durch Hinzufügen
weiterer Kreise sättigen können, dürfen wir o.B.d.A. stets
annehmen, daß bereits eine gesättigte Unterdeckung vorliegt.
Die Standardtriangulierung einer r-gesättigten Unterdeckung
soll im weiteren stets r-Triangulierung heißen, und besitzt
folgende Eigenschaften [70]:
- sie hat aufgrund des Euler'schen Polyedersatzes
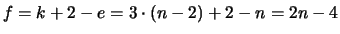 Dreiecke.
Dreiecke.
- Ein Umkreis eines Triangulierungsdreieckes kann keine
weiteren Ecken des Mosaikes als innere Punkte enthalten.
- Ist
 die Diagonale eines sphärischen Quadrates mit
Seitenlänge 2r, so müssen zwei Punkte mit Abstand kleiner
die Diagonale eines sphärischen Quadrates mit
Seitenlänge 2r, so müssen zwei Punkte mit Abstand kleiner
 auf derselben Dreiecksseite liegen.,
auf derselben Dreiecksseite liegen.,
- Ein zulässiges Dreieck hat Seiten
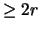 und Umkreisradius
kleiner
und Umkreisradius
kleiner 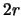 ; es gilt auch die Umkehrung.
; es gilt auch die Umkehrung.
- Bezeichnen wir mit
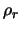 den Winkel eines gleichseitigen
Dreieckes mit Seitenlänge 2r. [Aus dem sphärischen
Kosinussatz folgt die Formel
den Winkel eines gleichseitigen
Dreieckes mit Seitenlänge 2r. [Aus dem sphärischen
Kosinussatz folgt die Formel
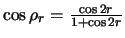 ],
so kann man beweisen, daß der Winkel eines zulässigen Dreieckes stets
zwischen
],
so kann man beweisen, daß der Winkel eines zulässigen Dreieckes stets
zwischen 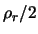 und
und 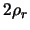 liegen muß, ohne allerdings die
Werte
liegen muß, ohne allerdings die
Werte 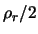 und
und 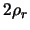 erreichen zu können [70].
erreichen zu können [70].
Besitzt ein sphärisches Dreieck Seitenlängen 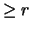 und einen
festen Winkel
und einen
festen Winkel 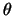 , so ist die kleinstmögliche Fläche des
Dreiecks gegeben durch:
, so ist die kleinstmögliche Fläche des
Dreiecks gegeben durch:
Hierbei bezeichnet
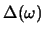 den Flächeninhalt eines
sphärischen, Dreieckes mit zwei Seiten der Länge 2r und dem von ihnen
eingeschlossenem Winkel
den Flächeninhalt eines
sphärischen, Dreieckes mit zwei Seiten der Länge 2r und dem von ihnen
eingeschlossenem Winkel 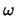 .
.
Die Funktion it A ist konkav in den Intervallen
[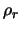 /2,
/2,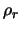 ] und [
] und [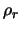 ,
,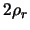 ]
und kann daher ihren Minimalwert nur an den Stellen
]
und kann daher ihren Minimalwert nur an den Stellen
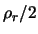 ,
, 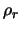 oder
oder 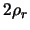 annehmen.
Da
annehmen.
Da
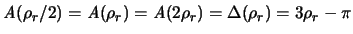 ist und da [ s.(v)] von diesen drei Werten nur
ist und da [ s.(v)] von diesen drei Werten nur
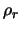 auftreten kann, ist unter allen gleichschenkeligen Dreiecken
das gleichseitige das Dreieck, das die kleinste Fläche besitzt.
Diese Fläche werden wir im weiteren stets mit
auftreten kann, ist unter allen gleichschenkeligen Dreiecken
das gleichseitige das Dreieck, das die kleinste Fläche besitzt.
Diese Fläche werden wir im weiteren stets mit
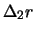 [=
[=
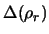 =
= 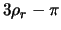 ] bezeichnen.
] bezeichnen.
Da die r-Triangulierung [ s.(i)] aus 2n-4 Dreiecken besteht,
und da '' Anzahl der Dreiecke mal Minimalfläche'' kleiner gleich
der Kugeloberfläche 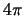 sein muß, folgt:
sein muß, folgt:
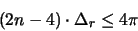 |
(1.5) |
Wir setzen in diese Ungleichung
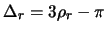 ein und erhalten:
ein und erhalten:
Wegen
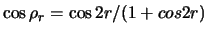 erhalten wir aus
erhalten wir aus
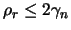 :
:
Zusammenfassend erhalten wir die Ungleichung von Fejes-Tóth für
den sphärischen Abstand in einer Unterdeckung [29], [30]:
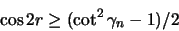 |
(1.6) |
Diese Ungleichung besagt für den sphärischen Minimalabstand 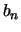 :
:
 |
(1.7) |
Wählt man die n Punkte jedoch aus einer unendlichen Folge
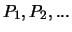 auf
auf 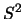 aus, so gilt für deren sphärischen Minimalabstand
aus, so gilt für deren sphärischen Minimalabstand 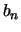 [35]:
[35]:
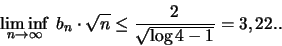 |
(1.8) |
Für die Ungleichung (2) gibt es zumindest fünf verschiedene
Beweise [29,30,39,70], darunter folgende zwei:
( 1) Wir zerlegen die Sphäre in Dirichlet'sche Zellen und wenden
den auf das dadurch erhaltene Dreikantmosaik folgende Ungleichung an:
Es seien 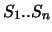 die Flächen eines Mosaikes,
die Flächen eines Mosaikes, 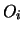 sei ein Punkt
der Fläche
sei ein Punkt
der Fläche 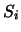 . Weiters bezeichne e die Anzahl der Ecken und
k die Anzahl der Kanten des Mosaikes.
D = D(ABC) sei ein Dreieck mit den Ecken A, B, C und den
zugehörigen Winkeln
. Weiters bezeichne e die Anzahl der Ecken und
k die Anzahl der Kanten des Mosaikes.
D = D(ABC) sei ein Dreieck mit den Ecken A, B, C und den
zugehörigen Winkeln
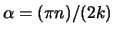 ,
,
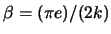 und
und
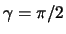 .
g sei eine auf
.
g sei eine auf ![$[0,\pi]$](img96.gif) definierte, nicht-zunehmende Funktion
und dP das Flächenelement des variablen Punktes P. Dann gilt:
definierte, nicht-zunehmende Funktion
und dP das Flächenelement des variablen Punktes P. Dann gilt:
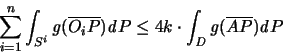 |
(1.9) |
Ist g nicht-abnehmend, so gilt die Ungleichung in umgekehrter
Richtung.]
Wir setzen
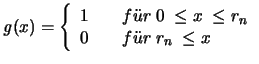 und verwenden das Dreikantmosaik der Dirichlet'schen Zellen
und verwenden das Dreikantmosaik der Dirichlet'schen Zellen 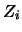 der Kreismittelpunkte
der Kreismittelpunkte 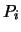 einer Lagerung mit Radius
einer Lagerung mit Radius 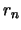 .
.
Da für alle Punkte, die sich nicht in einem Kreis der
Lagerung befinden, g Null wird, wird derjenige Teil der
Kugeloberfläche, der durch 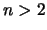 Kreise vom Radius
Kreise vom Radius 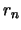 überdeckt
wird, dargestellt durch:
überdeckt
wird, dargestellt durch:
Analog dazu wird derjenige Teil des Dreieckes D = D(ABC),
der durch einen um den Punkt A geschlagenen Kreis mit Radius 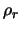 überdeckt wird, dargestellt durch:
überdeckt wird, dargestellt durch:
Klarerweise besitzt das Dreieck D die Winkel 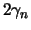 ,
,
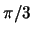 und
und 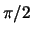 .
.
Bezeichnen wir mit D auch den Flächeninhalt des Dreieckes D,
so erhalten wir aus
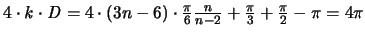 und der Ungleichung (2) die Ungleichung :
und der Ungleichung (2) die Ungleichung :
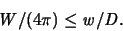 |
(1.10) |
Liegt eine Überdeckung mit Radius 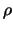 vor, so enthält der Kreis
um A mit Radius
vor, so enthält der Kreis
um A mit Radius 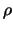 das ganze Dreieck D und es gilt
das ganze Dreieck D und es gilt
Diese Ungleichung enthält eine Abschätzung für 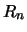 und
und 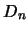 .
.
Analogerweise erhält man aus (6) eine Abschätzung für ein
Unterdeckung mit Radius 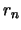 und Dichte
und Dichte 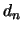 .
.
Diese Abschätzungen lauten nach Umformungen mit Formeln der
sphärischen Trigonometrie [man beachte, daß
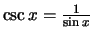 ]:
]:
- für das Unterdeckungsproblem :
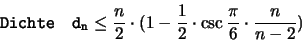 |
(1.11) |
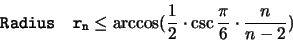 |
(1.12) |
- für das Überdeckungsproblem :
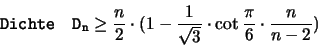 |
(1.13) |
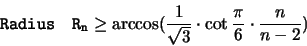 |
(1.14) |
( 2) Zu den bisherigen Konstruktionsmethoden eines sphärischen
Mosaikes soll noch eine Methode angegeben werden, die auf jedem
Raum konstanter Krümmung definiert ist [30, S.224ff]:
Wir denken uns auf der Kugel eine Lagerung von Kreisen mit
Mittelpunkten  usw. gegeben.
Liegt eine Unterdeckung vor, so können wir o.B.d.A.
voraussetzen, daß sie gesättigt ist, liegt eine Überdeckung vor, so
können wir o.B.d.A. annehmen, daß die Kreise sich nirgends
häufen, da wir ansonsten eine unendliche Dichte hätten.
Einen Kreis, der in seinem Inneren keinen, auf seinem Rand
aber zumindest drei der Kreismittelpunkte
usw. gegeben.
Liegt eine Unterdeckung vor, so können wir o.B.d.A.
voraussetzen, daß sie gesättigt ist, liegt eine Überdeckung vor, so
können wir o.B.d.A. annehmen, daß die Kreise sich nirgends
häufen, da wir ansonsten eine unendliche Dichte hätten.
Einen Kreis, der in seinem Inneren keinen, auf seinem Rand
aber zumindest drei der Kreismittelpunkte  enthält,
wollen wir Stützkreis nennen. Die auf seinem Rand liegenden
Kreismittelpunkte spannen ein konvexes Polygon, das Stützpolygon
auf. Durch diese Polygone definieren wir nun iterativ ein
Mosaik auf der Sphäre :
enthält,
wollen wir Stützkreis nennen. Die auf seinem Rand liegenden
Kreismittelpunkte spannen ein konvexes Polygon, das Stützpolygon
auf. Durch diese Polygone definieren wir nun iterativ ein
Mosaik auf der Sphäre :
Ist AB Seite eines Stützpolygons, so liegt in der Halbkugel,
die durch die Trägergerade von AB begrenzt wird, außer A und B
mindestens noch ein weiterer Kreismittelpunkt C der Lagerung.
Durch A, B und C muß es daher einen Stützkreis geben, und
dadurch können wir an jede Seite des Ausgangspolygons ein weiteres
Stützpolygon anschließen.
Zwei Stützpolygone greifen niemals übereinander. Denn
einerseites können sich - aufgrund der Definition - die zugehörigen
Stützkreise einander nicht enthalten, andererseits gibt es in
ihrem Schnitt nur zwei Punkte A und B (das sind die
Schnittpunkte der Kreisränder), die Kreismittelpunkte und somit
Mosaikeckpunkte sein können. Daher werden die Stützpolygone durch
die Gerade AB getrennt.
Starten wir bei einem beliebigen Stützpolygon und addieren
auf jeder '' freien'' Seite ein weiteres, so muß dieser Prozeß
abbrechen, sobald wir wieder '' in die Nähe'' des Ausgangspolygons
kommen, da ansonsten die Packung entweder nicht gesättigt wäre,
oder einen Häufungspunkt besitzen müßte [30].
Nun untersuchen wir noch den Gleichheitfall in (1): Da das
Dreieck mit kleinstem Flächeninhalt das gleichseitige Dreieck
ist, kann in (1) das Gleichheitszeichen nur von
Triangulierungen, die nur aus gleichseitigen Dreiecken bestehen,
eingenommen werden.
Solche Triangulierungen entstehen nur aus den regulären
Dreieckspolyedern. Daher sind optimale Punktanordnungen:
| für n = 3: |
Ecken eines regulären Dreieckes, |
|
| für n = 4: |
Ecken des regulären Tetraeders, |
|
| für n = 6: |
Ecken des regulären Oktoeders, |
|
| für n = 12: |
Ecken des regulären Ikosaeders |
|
Da die Ungleichung (1) auch für das Überdeckungsproblem gilt
[29], sind diese vier Anordnungen für beide Problemstellungen
optimal. Es wurde bewiesen [31], daß es nur endlich viele
natürliche Zahlen mit dieser Eigenschaft geben kann. Allerdings
wurde bisher keine weitere Zahl, die diese Bedingungen erfüllt,
entdeckt. Daher wird vermutet, daß die obigen vier Werte die
einzigen Zahlen mit dieser Eigenschaft sind.
Nun könnte man aber nicht nur versuchen, Ungleichungen für
den sphärischen Mindestabstand [wie
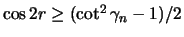 ]
herzuleiten, sondern sich auch die Frage stellen, wie die (sphärischen)
Abstände, die keine Mindestabstände sind, abgeschätzt werden können.
]
herzuleiten, sondern sich auch die Frage stellen, wie die (sphärischen)
Abstände, die keine Mindestabstände sind, abgeschätzt werden können.
Andreás und Károly Bezdek [5] haben den zweitnächsten Abstand
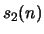 untersucht und bewiesen, daß gilt [ [x] sei das größte
Ganze von x]:
untersucht und bewiesen, daß gilt [ [x] sei das größte
Ganze von x]:




Nächste Seite: Halbreguläre Lagerungen
Aufwärts: Lagerungen auf der 3-Sphäre
Vorherige Seite: Aus der Polyedergeometrie
Inhalt
2004-03-25
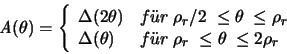
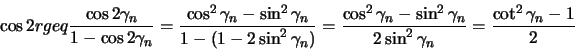
![]() die Flächen eines Mosaikes,
die Flächen eines Mosaikes, ![]() sei ein Punkt
der Fläche
sei ein Punkt
der Fläche ![]() . Weiters bezeichne e die Anzahl der Ecken und
k die Anzahl der Kanten des Mosaikes.
D = D(ABC) sei ein Dreieck mit den Ecken A, B, C und den
zugehörigen Winkeln
. Weiters bezeichne e die Anzahl der Ecken und
k die Anzahl der Kanten des Mosaikes.
D = D(ABC) sei ein Dreieck mit den Ecken A, B, C und den
zugehörigen Winkeln
![]() ,
,
![]() und
und
![]() .
g sei eine auf
.
g sei eine auf ![]() definierte, nicht-zunehmende Funktion
und dP das Flächenelement des variablen Punktes P. Dann gilt:
definierte, nicht-zunehmende Funktion
und dP das Flächenelement des variablen Punktes P. Dann gilt:
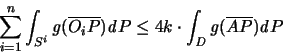
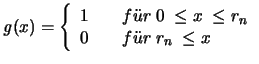 und verwenden das Dreikantmosaik der Dirichlet'schen Zellen
und verwenden das Dreikantmosaik der Dirichlet'schen Zellen 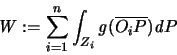
![]() usw. gegeben.
Liegt eine Unterdeckung vor, so können wir o.B.d.A.
voraussetzen, daß sie gesättigt ist, liegt eine Überdeckung vor, so
können wir o.B.d.A. annehmen, daß die Kreise sich nirgends
häufen, da wir ansonsten eine unendliche Dichte hätten.
Einen Kreis, der in seinem Inneren keinen, auf seinem Rand
aber zumindest drei der Kreismittelpunkte
usw. gegeben.
Liegt eine Unterdeckung vor, so können wir o.B.d.A.
voraussetzen, daß sie gesättigt ist, liegt eine Überdeckung vor, so
können wir o.B.d.A. annehmen, daß die Kreise sich nirgends
häufen, da wir ansonsten eine unendliche Dichte hätten.
Einen Kreis, der in seinem Inneren keinen, auf seinem Rand
aber zumindest drei der Kreismittelpunkte ![]() enthält,
wollen wir Stützkreis nennen. Die auf seinem Rand liegenden
Kreismittelpunkte spannen ein konvexes Polygon, das Stützpolygon
auf. Durch diese Polygone definieren wir nun iterativ ein
Mosaik auf der Sphäre :
enthält,
wollen wir Stützkreis nennen. Die auf seinem Rand liegenden
Kreismittelpunkte spannen ein konvexes Polygon, das Stützpolygon
auf. Durch diese Polygone definieren wir nun iterativ ein
Mosaik auf der Sphäre :